题目内容
如图所示，一杂技运动员骑摩托车沿一竖直圆轨道做特技表演，若摩托车运动的速率恒为v=20m/s，人和车的总质量为m=200kg，摩托车受到的阻力是摩托车对轨道压力的k倍，且k=0.1。摩托车通过最高点A时发动机的功率为零，(摩托车车身的长不计，取g=10 m/s2) 试求：⑴.竖直圆轨道的半径。⑵.摩托车通过最低点B时发动机的功率。
解：(1)由于车在A点时的功率为0，故车在A点时受到的牵引力、阻力和轨道对摩托车的弹力均为0。由牛顿运动定律得 mg=mv2/R------故, R=40m ------- （2）设摩托车在最低点B点时，轨道对它的弹力为NB，由牛顿运动定律得： NB－mg=mv2/R 所以，NB＝4000N ----- 又，摩托车在B点时受到的阻力为：f=kN=400N------ 则发动机的牵引力为: F=f=400N------------ 故摩托车在B点时的功率为: P=Fv=8000W------
练习册系列答案
相关题目
如图所示，一根跨越光滑定滑轮的轻绳，两端各有一杂技演员（可视为质点），a站于地面，b从图示的位置由静止开始向下摆动，运动过程中绳始终处于伸直状态，当演员b摆至最低点时，a刚好对地面无压力，则演员a质量与演员b质量之比为（ ）
（选修3-5）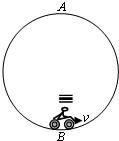
如图所示，一杂技运动员骑摩托车沿着一竖直圆轨道做特技表演，若摩托车运动的速率恒为v=20m/s，人和车的总质量为m=200m/s，摩托车受到的阻力是摩托车对轨道压力的k倍，且k=0.1．摩托车通过最高点A时发动机的功率为零，（摩托车车身的长不计，g=10m/s2）求：