题目内容
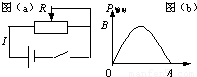
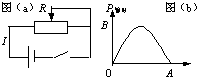图a为某一闭合电路，图b是该电路中总电流I与外电阻上输出功率P输出的关系曲线，若电路中电源电动势ε和内电阻r恒定，则I与P输出的函数关系式P输出=?I-I2r
?I-I2r
，图b中A点处电流值| ? |
| r |
| ? |
| r |
| ?2 |
| 4r |
| ?2 |
| 4r |
分析：电阻上输出功率P输出的于电源的总功率?I与电源内部分发热功率I2r之差．A点处P输出=0，B点处输出功率最大，由数学知识求解．
解答：解：根据功率的分配关系得：P输出=?I-I2r…①
A点处P输出=0，即有?I-I2r=0，解得，I=
B点处输出功率最大，
因P输出=?I-I2r=-rI2+?I，由数学知识得：当I=-
=-
=
时，P输出最大，
最大值为P输出max=??
-（
）2r=
故答案为：?I-I2r，
，
A点处P输出=0，即有?I-I2r=0，解得，I=
| ? |
| r |
B点处输出功率最大，
因P输出=?I-I2r=-rI2+?I，由数学知识得：当I=-
| b |
| 2a |
| ? |
| 2(-r) |
| ? |
| 2r |
最大值为P输出max=??
| ? |
| 2r |
| ? |
| 2r |
| ?2 |
| 4r |
故答案为：?I-I2r，
| ? |
| r |
| ?2 |
| 4r |
点评：本题一方面要知道电源的总功率、输出功率和内部发热功率的关系，另一方面要会运用数学知识求解极值．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，直线a为某一电源的U-I关系图线，直线b为某一定值电阻的U-I关系图线，则可知电源的内电阻为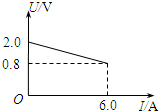
如图所示为某一闭合电路的路端电压U-I曲线，由图可知（ ）
