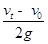题目内容
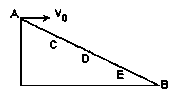
（8分）如图所示，位于竖直平面上的
圆弧轨道光滑，半径为R，OB沿竖直方向，上端A距地面高度为H，质量为m的小球从A点由静止释放，到达B点时的速度为
，最后落在地面上C点处，不计空气阻力．
求：（1）小球刚运动到B点时的加速度为多大，对轨道的压力多大．
（2）小球落地点C与B点水平距离为多少．
圆弧轨道光滑，半径为R，OB沿竖直方向，上端A距地面高度为H，质量为m的小球从A点由静止释放，到达B点时的速度为，最后落在地面上C点处，不计空气阻力．求：（1）小球刚运动到B点时的加速度为多大，对轨道的压力多大．
（2）小球落地点C与B点水平距离为多少．
（1）aB＝2g（2分）；3 mg（3分）；（2）s＝2
（3分）
（3分）试题分析：（1）由于小球到B点时的速度为
，再由牛顿第二定律可得，小球此时受到的向心力为F向＝m
＝maB（1分），故加速度为aB＝＝2g（1分）；对小球受力分析可得，FN－mg=maB＝2mg（2分）
故小球运动到B点对轨道的压力为FN ="3" mg（1分）。
（2）小球从B点被水平抛出时，竖直方向为自由落体运动，即：
（1分）水平方向为匀速直线运动，即s＝vBt （1分）
联立以上两式，解之得：s＝2
（1分）
练习册系列答案
相关题目
（n＝0，1，2，¼）
（n＝0，1，2，¼）
，落地速度为
，不计空气阻力，则物体在空中飞
