题目内容
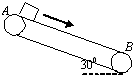 一物体质量为1kg,沿倾角为300的传送带从最高端A点以初速度v0=8m/s下滑,传送带匀速向下运动的速度为2m/s,全长20m.物体与传送带之间的动摩擦因数为
一物体质量为1kg,沿倾角为300的传送带从最高端A点以初速度v0=8m/s下滑,传送带匀速向下运动的速度为2m/s,全长20m.物体与传送带之间的动摩擦因数为
| ||
| 2 |
分析:判断出物体开始下滑的摩擦力,根据牛顿第二定律求出运动的加速度,得出速度达到2m/s时的位移,判断有无到达底端,因为滑动摩擦力小于重力的分力,所以速度相等后,一起做匀速直线运动.求出物体和传送带之间的相对位移,根据Q=f△x求出摩擦产生的热量.
解答:解:物体开始下滑的加速度a=
=gsin30°-μgcos30°=-2.5m/s2,知方向沿斜面向上.
当速度减小到2m/s时,位移x=
=
m=12m<20m.
因为滑动摩擦力小于重力的分力,所以速度相等后,一起做匀速直线运动.则物体运动到底端B点的速度大小为2m/s.
在速度相等前发生相对滑动,时间t=
=2.4s.
传送带的位移x′=v0t=8×2.4m=19.2m.
则相对滑动的位移△x=19.2-12m=7.2m
则Q=μmgcosθ△x=
×10×
×7.2J=54J.
故答案为:2,54.
| mgsin30°-μmgcos30° |
| m |
当速度减小到2m/s时,位移x=
| v2-v02 |
| 2a |
| 4-64 |
| -5 |
因为滑动摩擦力小于重力的分力,所以速度相等后,一起做匀速直线运动.则物体运动到底端B点的速度大小为2m/s.
在速度相等前发生相对滑动,时间t=
| v-v0 |
| a |
传送带的位移x′=v0t=8×2.4m=19.2m.
则相对滑动的位移△x=19.2-12m=7.2m
则Q=μmgcosθ△x=
| ||
| 2 |
| ||
| 2 |
故答案为:2,54.
点评:解决本题的关键能够通过物体的受力,判断物体的运动,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
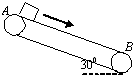
 ,物体运动到传送带底端B点的速度大小为 m/s;全过程中因物体和传送带间的摩擦而产生的热量为 J.(重力加速度g=10m/s2)
,物体运动到传送带底端B点的速度大小为 m/s;全过程中因物体和传送带间的摩擦而产生的热量为 J.(重力加速度g=10m/s2)