题目内容
20.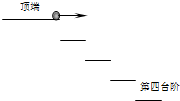 如图所示,一个小球从楼梯顶部以v0的速度水平抛出,每个台阶高度均为h,宽度均为L,欲使小球落在第四个台阶上,初速度应满足的条件为( )
如图所示,一个小球从楼梯顶部以v0的速度水平抛出,每个台阶高度均为h,宽度均为L,欲使小球落在第四个台阶上,初速度应满足的条件为( )| A. | $\frac{L}{2h}$$\sqrt{3gh}$<v0<$\frac{L}{2h}$$\sqrt{4gh}$ | B. | $\frac{L}{2h}$$\sqrt{3gh}$<v0<$\frac{L}{2h}$$\sqrt{5gh}$ | C. | $\frac{L}{2h}$$\sqrt{6gh}$<v0<$\frac{L}{2h}$$\sqrt{7gh}$ | D. | $\frac{L}{2h}$$\sqrt{6gh}$<v0<$\frac{L}{2h}$$\sqrt{8gh}$ |
分析 小球做平抛运动,水平方向上做匀速直线运动,竖直方向上做自由落体运动.要使小球落在第四个台阶上,水平位移的范围为3L<x<4L:结合两个临界状态,根据平抛运动的规律求出初速度范围.
解答 解:若小球打在第三个台阶的右边缘上,则 h1=3h
根据h1=$\frac{1}{2}$gt12,则t1=$\sqrt{\frac{6h}{g}}$,此时的初速度v1=$\frac{3L}{{t}_{1}}$=$\frac{L}{2h}$$\sqrt{6gh}$
若小球打在第四个台阶的右边缘上,则h2=4h.
由h2=$\frac{1}{2}$gt22,则t2=$\sqrt{\frac{8h}{g}}$,此时的初速度v2=$\frac{4L}{{t}_{2}}$=$\frac{L}{2h}$$\sqrt{8gh}$
则初始速度的范围为$\frac{L}{2h}$$\sqrt{6gh}$<v0<$\frac{L}{2h}$$\sqrt{8gh}$
故选:D.
点评 解决本题的关键掌握临界情况,结合平抛运动水平方向和竖直方向上的运动规律进行求解.

练习册系列答案
相关题目
11. 如图所示,将一条形磁铁N极向下插入一闭合的螺线管中的过程中,螺线管中产生感应电流,则下列说法正确的是( )
如图所示,将一条形磁铁N极向下插入一闭合的螺线管中的过程中,螺线管中产生感应电流,则下列说法正确的是( )
 如图所示,将一条形磁铁N极向下插入一闭合的螺线管中的过程中,螺线管中产生感应电流,则下列说法正确的是( )
如图所示,将一条形磁铁N极向下插入一闭合的螺线管中的过程中,螺线管中产生感应电流,则下列说法正确的是( )| A. | 螺线管中磁通量变小 | B. | 感应电流产生的磁场方向向下 | ||
| C. | 流过电流表的电流是由上向下 | D. | 流过电流表的电流是由下向上 |
5.堵住打气筒的出气口,缓慢向下压活塞使气体体积减小,你会感到越来越费力,温度保持不变.对这一现象的解释正确的是( )
| A. | 气体的密度增大,使得在相同时间内撞击活塞的气体分子数目增多 | |
| B. | 分子间没有可压缩的间隙 | |
| C. | 压缩气体要克服分子力做功 | |
| D. | 分子间相互作用力表现为引力 | |
| E. | 在压缩过程中,气体分子势能减小 |
12.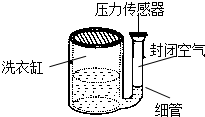 如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位逐渐升高,则细管中被封闭的空气( )
如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位逐渐升高,则细管中被封闭的空气( )
 如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位逐渐升高,则细管中被封闭的空气( )
如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位逐渐升高,则细管中被封闭的空气( )| A. | 气体的内能增大 | B. | 分子运动的平均动能增加 | ||
| C. | 气体一直向外界放热 | D. | 气体一直对外界做功 |
 如图所示,以水平方向为x轴,竖直方向为y轴在垂直平面建立平面直角坐标xOy,平行于x轴的虚线l1交y轴于P(0,d),平行于y轴的虚线l2交l1于Q(2d,d),今有比荷为k的两带正电小球A、B,虚线l1下方存在一竖直向上的匀强电场E1=$\frac{2g}{k}$(电场边界不含线l1),在虚线l1上方(电场边界含l1)存在一向左上方的匀强电场E2(未知),小球A自O以某一水平向右的初速度释放,与此同时,小球B自P点以水平向右的初速度v0=3$\sqrt{2gd}$.释放后恰沿虚线l1运动,运动中不考虑带电小球间相互作用及小球电荷电荷量对电场分布的影响.
如图所示,以水平方向为x轴,竖直方向为y轴在垂直平面建立平面直角坐标xOy,平行于x轴的虚线l1交y轴于P(0,d),平行于y轴的虚线l2交l1于Q(2d,d),今有比荷为k的两带正电小球A、B,虚线l1下方存在一竖直向上的匀强电场E1=$\frac{2g}{k}$(电场边界不含线l1),在虚线l1上方(电场边界含l1)存在一向左上方的匀强电场E2(未知),小球A自O以某一水平向右的初速度释放,与此同时,小球B自P点以水平向右的初速度v0=3$\sqrt{2gd}$.释放后恰沿虚线l1运动,运动中不考虑带电小球间相互作用及小球电荷电荷量对电场分布的影响.