Question

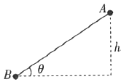
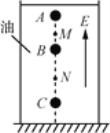
【题目】如图所示，质量为电荷量为的带正电小球A穿在光滑绝缘细杆(固定)上，杆的倾角为在杆的底端B固定一电荷量为的带负电小球，将A球从杆的顶端(距B高为处)由静止释放，当A球运动到杆的中点时速度大小为整个装置处于真空中，已知重力加速度为静电力常量为求:

(1)A球刚被释放时的加速度大小

(2)在从释放A球到其运动到杆的中点的过程中静电力做的功W.

Answer 1

【答案】（1）A球刚释放时的加速度大小是gsinθ；（2）在从释放A球到其运动到杆的中点的过程中，静电力做的功为。

【解析】

由题图可知，考查了牛顿第二定律，动能定理以及库伦定律。结合相应的知识即可求解：

（1）对A球受力分析，受到重力、支持力和静电斥力，根据牛顿第二定律求加速度；

（2）根据动能定理，结合重力做功，与A球运动到细杆的中点时速度大小，即可求解。

（1）由牛顿第二定律可知mgsin θ+F＝ma

根据库仑定律F＝k

又据几何关系有r

解得a＝gsinθ

（2）由动能定理，则有：W+mg

解得：W