题目内容
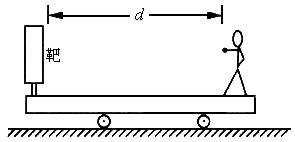
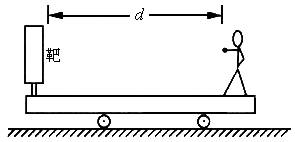
小车静置在光滑水平面上，站在车上的人练习打靶，靶装在车上的另一端，如图所示，已知车、人、枪和靶的总质量为M（不含子弹），每颗子弹质量为m，共n发。打靶时，每发子弹打入靶中，就留在靶里，且待前一发打入靶中后，再打下一发。若枪口到靶的距离为d，待打完n发子弹后，小车移动的距离为多少？
答案：见详解
解析：
解析：
解：第一，车、人、靶与子弹构成的系统总动量守恒，且总动量为零；第二，质量为m的子弹以速度为v发射后，小车[质量为M+(n-1)m]应具有反冲速度v车，就构成了靶以速度v车与子弹（速度v）的相遇问题，即它们位移的代数和等于d；第三，子弹打入靶后，整个系统具有相同的速度，且这个速度一定为零。通过分析，得到本题的两个基本解法：其一，只要求出打一子弹后的小车的位移，再乘以n即可；其二，可等效为n发子弹一起发出，所得的结果相同，现采用第二种解法由动量守恒得nmv=Mv车，
|
，又s+s车=d，所以
得
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
