题目内容
7. 如图所示,两比荷相同的微粒在同一匀强磁场(磁场未画出)中垂直磁感线做匀速圆周运动,已知两微粒转向相反,RA>RB,则可判定两微粒所带电荷电性相反(填相同或相反);两微粒运动周期TA=TB(填>、<或=);两微粒运动速度大小VA>VB(填>、<或=).
如图所示,两比荷相同的微粒在同一匀强磁场(磁场未画出)中垂直磁感线做匀速圆周运动,已知两微粒转向相反,RA>RB,则可判定两微粒所带电荷电性相反(填相同或相反);两微粒运动周期TA=TB(填>、<或=);两微粒运动速度大小VA>VB(填>、<或=).
分析 粒子进入磁场后受到洛伦兹力而偏转,根据轨迹偏转的方向确定出洛伦兹力的方向,由左手定则判断粒子的电性.根据轨迹半径公式r=$\frac{mv}{qB}$分析速度的大小.
解答 解:A粒子沿顺时针方向偏转,B粒子沿逆时针方向偏转,说明二者所受的洛伦兹力相反,根据左手定则判断可知A与B的电性一定相反.
根据洛伦兹力提供向心力可知:$qvB=\frac{m{v}^{2}}{r}$,粒子的半径:$r=\frac{mv}{qB}=\frac{1}{B}•\frac{m}{q}•v$,由于两个微粒的比荷相同,所以二者的半径都与速度成正比,所以半径比较大的A的速度大,即VA>VB.
周期:$T=\frac{2πr}{v}=\frac{2πm}{qB}=\frac{2π}{B}•\frac{m}{q}$,由于两个微粒的比荷相同,所以二者的周期是相等的.
故答案为:相反,=,>
点评 该题考查带电微粒在磁场中的运动,解答的关键要掌握左手定则和半径公式、周期公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.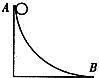 如图所示,物体沿曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5m,速度为6m/s,若物体的质量为1kg.则下滑过程中物体克服阻力所做的功为( )
如图所示,物体沿曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5m,速度为6m/s,若物体的质量为1kg.则下滑过程中物体克服阻力所做的功为( )
 如图所示,物体沿曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5m,速度为6m/s,若物体的质量为1kg.则下滑过程中物体克服阻力所做的功为( )
如图所示,物体沿曲面从A点无初速度滑下,滑至曲面的最低点B时,下滑的高度为5m,速度为6m/s,若物体的质量为1kg.则下滑过程中物体克服阻力所做的功为( )| A. | 50J | B. | 18J | C. | 32J | D. | 0J |
18.以下四个实验中,可能用到打点计时器的是( )
| A. | 验证力的平行四边形定则 | |
| B. | 探究加速度与物体质量、物体受力的关系 | |
| C. | 探究匀变速直线运动的规律 | |
| D. | 探究弹簧的弹力和弹簧伸长的关系 |
15.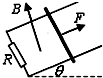 如图所示,下端接有电阻R的“U”形光滑金属导轨与水平面成θ角,导轨所在空间有一与导轨平面垂直的匀强磁场.导轨上有一个金属棒,金属棒与两导轨垂直且接触良好,在沿着斜面向上且与棒垂直的拉力F作用下,金属棒沿导轨匀速上滑,则下列说法正确的是( )
如图所示,下端接有电阻R的“U”形光滑金属导轨与水平面成θ角,导轨所在空间有一与导轨平面垂直的匀强磁场.导轨上有一个金属棒,金属棒与两导轨垂直且接触良好,在沿着斜面向上且与棒垂直的拉力F作用下,金属棒沿导轨匀速上滑,则下列说法正确的是( )
 如图所示,下端接有电阻R的“U”形光滑金属导轨与水平面成θ角,导轨所在空间有一与导轨平面垂直的匀强磁场.导轨上有一个金属棒,金属棒与两导轨垂直且接触良好,在沿着斜面向上且与棒垂直的拉力F作用下,金属棒沿导轨匀速上滑,则下列说法正确的是( )
如图所示,下端接有电阻R的“U”形光滑金属导轨与水平面成θ角,导轨所在空间有一与导轨平面垂直的匀强磁场.导轨上有一个金属棒,金属棒与两导轨垂直且接触良好,在沿着斜面向上且与棒垂直的拉力F作用下,金属棒沿导轨匀速上滑,则下列说法正确的是( )| A. | 拉力做的功等于该金属棒的机械能的增量 | |
| B. | 拉力做的功等于该金属棒重力势能的增量与回路产生的热量之和 | |
| C. | 该金属棒所受的拉力、安培力、重力做功之和等于回路产生的热量 | |
| D. | 安培力对该金属棒做的功的大小等于回路中产生的电能 |
2.在做“用单摆测定重力加速度的实验”中为了减小误差,应注意的事项如下,其中错误的是( )
| A. | 摆球以选密度大,体积小的小球为好 | |
| B. | 摆长以0.25米为宜 | |
| C. | 摆角应小于5° | |
| D. | 摆线的悬点要固定,方不会在摆动中出现移动或晃动 | |
| E. | 要使单摆在竖直平面内摆动,不得使其形成锥形摆或摆球转动 | |
| F. | 测量周期时,应从摆球通过最低点时开始计时 |
12.下列关于分子运动和热现象的说法正确的是( )
| A. | 温度升高,分子热运动的平均动能一定增大 | |
| B. | 在车胎突然爆裂后的瞬间,车胎内的气体膨胀对外做功 | |
| C. | 物体吸收热量,内能一定增加 | |
| D. | 所有涉及热现象的宏观自然过程都具有方向性 |
19.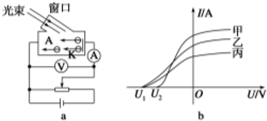 在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )
在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )
 在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )
在光电效应实验中,小明同学用同一实验装置(如图a)在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图b所示.则不正确的是( )| A. | 乙光的频率小于甲光的频率 | |
| B. | 甲光的波长大于丙光的波长 | |
| C. | 丙光的光子能量小于甲光的光子能量 | |
| D. | 乙光对应的光电子最大初动能小于丙光的光电子最大初动能 |
16.下列说法正确的是( )
| A. | 滑动摩擦力一定对物体做负功,静摩擦力一定对物体不做功 | |
| B. | 一对作用力与反作用力对物体做功的代数和一定为零 | |
| C. | 某力对物体做负功,可以说成“物体克服某力做功” | |
| D. | 一个受变力作用的物体做曲线运动时,其合力的瞬时功率不可能为零 |
17.关于电场线,下列说法中正确的是( )
| A. | 电场线是电场中实际存在的一些曲线 | |
| B. | 匀强电场的电场线是一组相互平行等间距的直线 | |
| C. | 两条电场线在电场中可以交于一点 | |
| D. | 电场线起始于负电荷,终止于正电荷 |