题目内容
两平行金属板间的电压为U,两板间距为d,一质量为m,电量为q的带电粒子以初速度v0垂直于电场线方向进入匀强电场,离开电场时,偏转距离为d/2,那么带电粒子离开电场时的动能为
qU+
m
.
qU+
m
. (粒子重力不计).
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
分析:带电粒子通过电场过程,电场力做功
qU,根据动能定理求解带电粒子离开电场时的动能.
| 1 |
| 2 |
解答:解:由题,带电粒子离开电场时,偏转距离为
d,而两平行金属板间的电压为U,两板间距为d,则离开电场和进入电场两点间电势差为
U,电场力做功为
qU,由动能定理得:
qU=Ek-
m
解得:Ek=
qU+
m
故答案为:
qU+
m
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得:Ek=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
点评:本题确定带电粒子离开电场和进入电场两点间电势差是关键.根据动能定理求解动能是常用方法.

练习册系列答案
相关题目
 如图甲所示,在两平行金属板的中线OO′某处放置一个粒子源,粒子沿OO1方向连续不断地放出速度
如图甲所示,在两平行金属板的中线OO′某处放置一个粒子源,粒子沿OO1方向连续不断地放出速度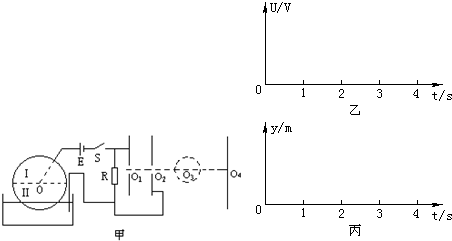 如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的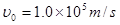 的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场,磁感应强度B=0.01
的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场,磁感应强度B=0.01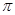 T,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比
T,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比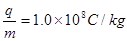 ,粒子的重力和粒子之间的作用力均可忽略不计,若
,粒子的重力和粒子之间的作用力均可忽略不计,若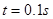 时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:
时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:
 的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场,磁感应强度B=0.01
的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场,磁感应强度B=0.01 T,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比
T,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比 ,粒子的重力和粒子之间的作用力均可忽略不计,若
,粒子的重力和粒子之间的作用力均可忽略不计,若 时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:
时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求: