题目内容
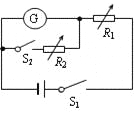
【题目】如图甲所示在光滑水平面上轻质弹簧一端固定。物体A以速度v0向右运动压缩弹簧测得弹簧的最大压缩量为x。现让该弹簧一端连接另一质量为2m的物体B(如图乙所示),静止在水平面上。物体A以2v0的速度向右压缩弹簧测得弹簧的最大压缩量仍为x。则

A. A物体的质量为6m
B. A物体的质量为4m
C. 弹簧压缩最大时的弹性势能为![]()
D. 弹簧压缩最大时B的动量为![]()
【答案】ACD
【解析】
当弹簧固定时,当弹簧压缩量最大时,弹性势能最大,A的动能转化为弹簧的弹性势能,根据系统的机械能守恒得:弹簧被压缩过程中最大的弹性势能等于A的初动能,设A的质量为mA,即有:![]() ①
①
当弹簧一端连接另一质量为m的物体B时,A与弹簧相互作用的过程中B将向右运动,A、B速度相等时,弹簧的弹性势能最大,选取A的初速度的方向为正方向,由动量守恒定律得:mA2v0=(2m+mA)v,②
由机械能守恒定律得:![]() ③
③
联立得:mA=6m ④
联立①④得:Epm=3mv02
弹簧压缩最大时B的动量为2mv=3mv0
故ACD正确,B错误。

练习册系列答案
相关题目