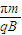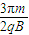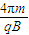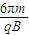题目内容
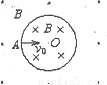
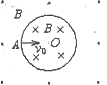
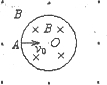如图所示，一空间内有磁感应强度大小均为B的两匀强磁场区域以半径为R的圆周为界，圆周内磁场方向垂直纸面向里，圆周外磁场方向垂直纸面向外且范围足够大．一质量为m，电量为q的粒子以速度v0，从圆周上的A点正对圆心O进入圆周内磁场，不许粒子重力和空气阻力，已知v0=
| qBR |
| m |
间t再次到达A点，则时间t至少为（ ）
分析：粒子在磁场中由洛伦兹力提供向心力，根据牛顿第二定律求出粒子在磁场中匀速圆周运动的半径和周期，画出轨迹，确定圆心角，求出时间．
解答：解：由牛顿第二定律，得：
qv0B=m
，得r=
，周期T=
将v0=
代入，得r=R
画出轨迹，粒子再次到达A点时，经过的最短时间为
t=2T=
故C正确．
故选C．
qv0B=m
| v02 |
| r |
| mv0 |
| qB |
| 2πm |
| qB |
将v0=
| qBR |
| m |
画出轨迹，粒子再次到达A点时，经过的最短时间为
t=2T=
| 4πm |
| qB |
故选C．
点评：带电粒子在匀强磁场中匀速圆周运动问题，关键是运用几何知识画轨迹，根据圆心角求解运动时间．
练习册系列答案
名校课堂系列答案
相关题目
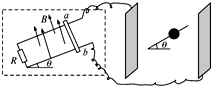如图所示在虚线空间内有一对彼此平行的金属导轨，宽为L，与水平面的夹角为θ，导轨电阻不计，在虚线空间内同时分布着垂直导轨平面向上的磁感应强度为B的匀强磁场．导轨的下端接一定值电阻R，上端通过导线与一对竖直放置的平行金属板相连接，两板间距为d，其间固定着一光滑绝缘直杆，它与水平面也成θ角，杆上套一带电小球．当一电阻也为R的光滑导体棒ab沿导轨以速度v匀速下滑时，小球恰好静止在绝缘直杆上．则由此可以判断小球的电性并能求出其荷质比为（ ）A、正电荷，
| ||
B、正电荷，
| ||
C、负电荷，
| ||
D、负电荷，
|
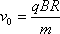，粒子经过时间t再次到达A点，则时间t至少为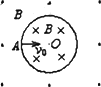
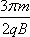
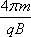
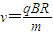，粒子经过时
