题目内容
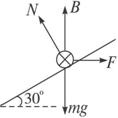
有一金属棒ab，质量为m，电阻不计，可在两条轨道上滑动，如图所示．轨道间距离为L，轨道平面与水平面夹角为θ，整个装置置于竖直向上的匀强磁场中，磁感应强度大小为B，金属棒与轨道的最大静摩擦力为重力的k倍，回路中电源电动势为E，内阻不计．问：（1）应把滑动变阻器阻值调节多大才能使金属棒保持静止而金属棒与轨道间的摩擦力恰好为零？
（2）若B的方向改为与轨道平面垂直斜向上，则滑动变阻器阻值调节在什么阻值范围内金属棒恰能静止在轨道上？
分析：（1）金属棒与轨道间的摩擦力恰好为零，此时金属棒受重力、支持力和向右的安培力，根据平衡条件求解安培力，然后根据安培力公式和闭合电路欧姆定律列式求解变阻器阻值；
（2）考虑金属棒恰好不下滑和恰好不上滑两种临界情况，受力分析后根据平衡条件求解安培力；然后结合安培力公式和闭合电路欧姆定律列式求解变阻器阻值的临界值，得到电阻值的范围．
（2）考虑金属棒恰好不下滑和恰好不上滑两种临界情况，受力分析后根据平衡条件求解安培力；然后结合安培力公式和闭合电路欧姆定律列式求解变阻器阻值的临界值，得到电阻值的范围．
解答：解：（1）若磁场竖直向上，安培力为水平方向，如图a所示，
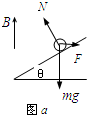
当mgsinθ=Fcosθ时，f=0，又因为：F=BIL=B
L，
所以mgsinθ=B
Lcosθ，得：R=
．
（2）若B的方向改为与轨道平面垂直斜向上
当安培力较小，物体恰好要沿斜面下滑时，金属棒受力如图b所示．
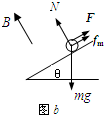
沿斜面方向：
F+fm=mgsinθ，
又F=BIL=B
L
fm=kmg
三式联立解得：
R=
．
当安培力较大，物体恰好要沿斜面上滑时，金属棒受力如图c所示
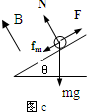
沿斜面方向：
F=fm+mgsinθ
又F=BIL=B
L
fm=kmg
三式联立解得：
R=
．
所以，当
≤R≤
时金属棒恰能静止在轨道上．
答：（1）应把滑动变阻器阻值调节到
时才能使金属棒保持静止而金属棒与轨道间的摩擦力恰好为零；
（2）若B的方向改为与轨道平面垂直斜向上，则滑动变阻器阻值调节在
≤R≤
阻值范围内金属棒恰能静止在轨道上．
当mgsinθ=Fcosθ时，f=0，又因为：F=BIL=B
| E |
| R |
所以mgsinθ=B
| E |
| R |
| BELcosθ |
| mgsinθ |
（2）若B的方向改为与轨道平面垂直斜向上
当安培力较小，物体恰好要沿斜面下滑时，金属棒受力如图b所示．
沿斜面方向：
F+fm=mgsinθ，
又F=BIL=B
| E |
| R |
fm=kmg
三式联立解得：
R=
| BEL |
| mgsinθ-kmg |
当安培力较大，物体恰好要沿斜面上滑时，金属棒受力如图c所示
沿斜面方向：
F=fm+mgsinθ
又F=BIL=B
| E |
| R |
fm=kmg
三式联立解得：
R=
| BEL |
| mgsinθ+kmg |
所以，当
| EBL |
| mgsinθ+kmg |
| EBL |
| mgsinθ-kmg |
答：（1）应把滑动变阻器阻值调节到
| BELcosθ |
| mgsinθ |
（2）若B的方向改为与轨道平面垂直斜向上，则滑动变阻器阻值调节在
| EBL |
| mgsinθ+kmg |
| EBL |
| mgsinθ-kmg |
点评：本题关键对三种临界情况受力分析，根据平衡条件求解出安培力，然后结合结合安培力公式和闭合电路欧姆定律列式求解变阻器阻值的临界值．
练习册系列答案
相关题目
如图所示，有一金属棒ab，质量m=5g，电阻R=0.1Ω，可以无摩擦地在两条轨道上滑行，轨道间的距离d=10cm，电阻不计，轨道平面与水平面间的夹角θ=53°，整个装置置于磁感应强度B=0.4T，方向竖直向上的匀强磁场中，回路中电源的电动势E=2V，内阻r=0.1Ω．求变阻器R0多大时，可使金属棒在轨道上保持静止（sin53°=0.8，cos53°=0.6）．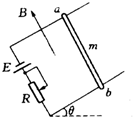
有一金属棒ab，质量为m，电阻不计，可在两条光滑的倾斜轨道上滑动．如图所示，轨道间距为L，其平面与水平面的夹角为θ，置于垂直于轨道平面向上的匀强磁场中，磁感应强度为B，回路中电源电动势为E，内阻不计．当滑动变阻器R阻值调节为