题目内容
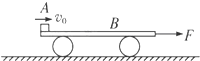 如图所示,物体A的质量M=1kg,静止在光滑水平面上的平板车B的质量为m=0.5kg、长为L=1m.某时刻物体A以v0=4m/s向右的初速度滑上木板B的上表面,在A滑上B的同时,给B施加一个水平向右的拉力F=5N.忽略物体A的大小,已知A与B之间的动摩擦因数μ=0.2,重力加速度取g=10m/s2,试求:
如图所示,物体A的质量M=1kg,静止在光滑水平面上的平板车B的质量为m=0.5kg、长为L=1m.某时刻物体A以v0=4m/s向右的初速度滑上木板B的上表面,在A滑上B的同时,给B施加一个水平向右的拉力F=5N.忽略物体A的大小,已知A与B之间的动摩擦因数μ=0.2,重力加速度取g=10m/s2,试求:
(1)物体A在平板车上经多长时间与平板车有相同的速度;
(2)物体A在小车上运动时相对小车向右滑行的最大距离.
解:(1)物体A滑上木板B以后,做匀减速运动,有?μmg=maA得aA=μg=2m/s2
木板B做加速运动,有F+μmg=MaB,得:aB=14m/s2
两者速度相同时,有v0-aAt=aBt得:t=0.25 s
(2)达到共同速度时,物体A在小车上运动时相对小车向右滑行的距离最大.
A滑行距离: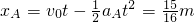
B滑行距离: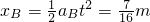
最大距离:△x=xA-xB=0.5m
答;(1)物体A在平板车上经0.25s与平板车有相同的速度;
(2)物体A在小车上运动时相对小车向右滑行的最大距离为0.5m.
分析:首先分析物体A和车的运动情况:A相对于地做匀减速运动,车相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,物体A在小车上运动时相对小车滑行的最大距离.由牛顿第二定律和运动学公式结合,以及速度相等的条件,分别求出A与车相对于地的位移,两者之差等于A在小车上运动时相对小车滑行的最大距离.
点评:牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件.
木板B做加速运动,有F+μmg=MaB,得:aB=14m/s2
两者速度相同时,有v0-aAt=aBt得:t=0.25 s
(2)达到共同速度时,物体A在小车上运动时相对小车向右滑行的距离最大.
A滑行距离:
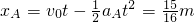
B滑行距离:
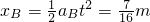
最大距离:△x=xA-xB=0.5m
答;(1)物体A在平板车上经0.25s与平板车有相同的速度;
(2)物体A在小车上运动时相对小车向右滑行的最大距离为0.5m.
分析:首先分析物体A和车的运动情况:A相对于地做匀减速运动,车相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,物体A在小车上运动时相对小车滑行的最大距离.由牛顿第二定律和运动学公式结合,以及速度相等的条件,分别求出A与车相对于地的位移,两者之差等于A在小车上运动时相对小车滑行的最大距离.
点评:牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件.

练习册系列答案
相关题目
 (2013?福州模拟)如图所示,物体A的质量是物体B的质量的2倍,中间压缩一轻质弹簧,放在光滑的水平面上,由静止同时放开两手后一小段时间内?( )
(2013?福州模拟)如图所示,物体A的质量是物体B的质量的2倍,中间压缩一轻质弹簧,放在光滑的水平面上,由静止同时放开两手后一小段时间内?( )


