Question

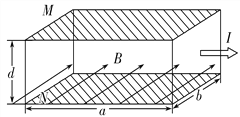
【题目】如图所示，光滑水平面上静置一质量为m、长为L的长木板B，木板上表 面各处粗糙程度相同，一质量为m的小物块A(可视为质点)从左端以速度v冲上木板，当v=v0时，小物块A历时t0恰好运动到木板右端与木板共速。此过程中A、B系统生热为Q，则( )

A. 若v=，A、B相对运动时间为

B. 若v=，A、B系统生热为

C. 若v=2v0，A经历达木板右端

D. 若v=2v0，A、B系统生热为Q

Answer 1

【答案】AD

【解析】

对于A、B组成的系统，由于系统所受的合外力为零，则系统的动量守恒，由动量守恒定律求出最终两者的共同速度，再由对B，运用动量定理求运动时间。由系统的能量守恒求系统生热。

A项：当v=v0时，取向右为正方向，根据动量守恒定律得：mv0=2mv′

代入数据得：v′=0.5v0

对B，由动量定理得：ft0=mv′

可得：

由能量守恒定律得：

若，取向右为正方向，根据动量守恒定律得：

解得：

对B，由动量定理得：

ft=mv′

解得：

可得：

AB系统生热，故A正确，B错误；

C、D项：若v=2v0，取向右为正方向，根据动量守恒定律得：

m2v0=mvA+mvB，

A、B系统生热等于系统克服摩擦力做功，与木板的长度有关，可知A、B系统生热仍为Q。

根据能量守恒定律得：

结合上面解答有：

对B，由动量定理得：

ft=mvB-0

联立解得： ，，故C错误，D正确。

故选：AD。