Question

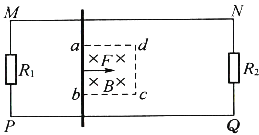
【题目】如图所示，光滑导轨MN和PQ固定在同一水平面上，两导轨间距为L，两端分别接有阻值均为R的定值电阻R1和R2．两导轨间有一边长为的正方形区域abcd，该区域内有方向竖直向下的匀强磁场，磁感应强度为B．一质量为m的金属杆与导轨接触良好并静止于ab处，现用一恒力F沿水平方向拉杆，使之由静止起向右运动，若杆出磁场前已做匀速运动，不计导轨及金属杆的电阻．求：

（1）金属杆出磁场前的瞬间流过R1的电流大小和方向；

（2）金属杆做匀速运动时的速率；

（3）金属杆穿过整个磁场过程中R1上产生的电热．

Answer 1

【答案】（1）金属杆出磁场前的瞬间流过的电流大小为，方向从M到P；

（2）金属杆做匀速运动时的速率是；

（3）金属杆穿过整个磁场过程中上产生的电热是﹣．

【解析】

试题（1）杆出磁场前已做匀速运动，恒力F与安培力平衡，由安培力公式F=BIL和平衡条件求解；

（2）杆产生的感应电动势E=Bv，又根据闭合欧姆定律得到E=I，联立可求得速度v；

（3）金属杆穿过整个磁场过程中，F做功为F，杆获得的动能为，根据能量守恒定律求解回路中产生的总热量，根据两个电阻并联求解上产生的电热．

解：（1）设流过金属杆中的电流为I，由平衡条件得：

F=BI

解得，I=

因=，所以流过的电流大小为I1==

根据右手定则判断可知，电流方向从M到P．

（2）设杆做匀速运动的速度为v，由法拉第电磁感应定律得：

杆切割磁感线产生的感应电动势大小为 E=Bv

又根据闭合欧姆定律得到E=I，

可解得v=

（3）设整个过程电路中产生的总电热为Q，根据能量守恒定律得：

Q=F﹣

代入v可得Q=﹣

∴Q1=Q=﹣

答：

（1）金属杆出磁场前的瞬间流过的电流大小为，方向从M到P；

（2）金属杆做匀速运动时的速率是；

（3）金属杆穿过整个磁场过程中上产生的电热是﹣．