题目内容
18.河宽300m,水流速度为3m/s,船在静水中的速度为6m/s,现令该船从岸边开始渡河,试问:(1)要求船以最短的时间渡河,实际将到达对岸的什么位置?
(2)要求船以最小的位移渡河时,船头朝向应与上游河岸成多大角度?
分析 (1)当静水速的方向与河岸方向垂直,此时渡河时间最短,此时船不仅参与了静水运动,还参与了水流运动,求出渡河时间,即可求出沿水流方向上的位移.
(2)当静水速与水流速的合速度方向垂直于河岸,船将沿垂直河岸方向运动,此时位移最短,根据t=$\frac{d}{{v}_{合}}$ 求出渡河时间.
解答 解:(1)若船以最短时间渡河,则船身必须垂直河岸过河,过河时间t=$\frac{d}{{v}_{c}}$=$\frac{300}{6}$=50s,船沿着水流方向走过的距离x=v水t=150m;所以船到达正对岸下游150m处;
(2)由于V船>V水,小船可以到达正对岸,最小位移为300m,
设船头偏向上游河岸成α角,则有:cosα=$\frac{{v}_{s}}{{v}_{c}}$=$\frac{3}{6}$=0.5.
解得:α=60°
答:(1)船渡河的最短时间为60s,船将到达正对岸下游180m处.
(2)船以最小的位移渡河时,船头朝向应与上游河岸成60°.
点评 解决本题的关键知道当静水速的方向与河岸垂直时,渡河时间最短;当静水速大于水流速,静水速与水流速的合速度方向与河岸垂直时,渡河位移最小.

练习册系列答案
相关题目
8. 如图所示,M、N为两个等量同种电荷,在其连线的中垂线上的P点放一个静止的点电荷q(负电荷),当把该点电荷释放,它只在电场力作用下运动时,下列说法正确的是( )
如图所示,M、N为两个等量同种电荷,在其连线的中垂线上的P点放一个静止的点电荷q(负电荷),当把该点电荷释放,它只在电场力作用下运动时,下列说法正确的是( )
 如图所示,M、N为两个等量同种电荷,在其连线的中垂线上的P点放一个静止的点电荷q(负电荷),当把该点电荷释放,它只在电场力作用下运动时,下列说法正确的是( )
如图所示,M、N为两个等量同种电荷,在其连线的中垂线上的P点放一个静止的点电荷q(负电荷),当把该点电荷释放,它只在电场力作用下运动时,下列说法正确的是( )| A. | 点电荷在从P到O的过程中,加速度越来越大,速度越来越大 | |
| B. | 点电荷在从P到O的过程中,加速度越来越小,速度越来越大 | |
| C. | 点电荷运动到O点时加速度为零,速度达最大值 | |
| D. | 点电荷越过O点后,速度越来越小,加速度越来越大,直到速度为零 |
9.关于气体压强和热力学定律,以下理解不正确的是( )
| A. | 从微观上讲,气体的压强是大量的气体分子无规则运动不断撞击器壁产生的 | |
| B. | 只从单一热源吸热,使之完全变为有用功而不产生其他影响的机器是可以制造出来的 | |
| C. | 温度升高时,气体的压强一定增大 | |
| D. | 绝对零度不可达到 |
10.对曲线运动说法正确的是( )
| A. | 路线是直的 | |
| B. | 是变速运动 | |
| C. | 某点的速度方向沿曲线在这点的切线方向 | |
| D. | 不受外力 |
7.静电场方向平行于x轴,其电势φ随的分布可简化为如图所示的折线,下列说法中正确的是( )
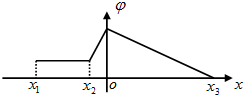

| A. | x轴上x2到O之间的电场强度大于O到x3之间的电场强度 | |
| B. | x轴上x2到O之间的电场强度的方向与O到x3之间的电场强度的方向相同 | |
| C. | 正电荷沿x轴从x1运动到O的过程中,电场力做正功,电势能减少 | |
| D. | 负电荷沿x轴从O运动到x3的过程中,电场力做负功,电势能增加 |
8. 跳伞表演是人们普遍喜欢的观赏性体育项目,如图所示,当运动员从直升机上由静止跳下后,在下落过程中将会受到水平风力的影响,下列说法中正确的是( )
跳伞表演是人们普遍喜欢的观赏性体育项目,如图所示,当运动员从直升机上由静止跳下后,在下落过程中将会受到水平风力的影响,下列说法中正确的是( )
 跳伞表演是人们普遍喜欢的观赏性体育项目,如图所示,当运动员从直升机上由静止跳下后,在下落过程中将会受到水平风力的影响,下列说法中正确的是( )
跳伞表演是人们普遍喜欢的观赏性体育项目,如图所示,当运动员从直升机上由静止跳下后,在下落过程中将会受到水平风力的影响,下列说法中正确的是( )| A. | 运动员下落时间与风力无关 | |
| B. | 运动员着地速度与风力无关 | |
| C. | 风力越大,运动员下落时间越长,运动员可完成更多的动作 | |
| D. | 风力越大,运动员着地速度越大,有可能对运动员造成伤害 |
 为了测定气垫导轨上滑块的加速度,滑块上安装了宽度为3.0cm的遮光板,如图所示,滑块在牵引力作用下先后匀加速通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1=0.30s,通过第二个光电门的时间为△t2=0.10s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t=3.0s.则滑块的加速度是0.067m/s2(结果保留2位有效数字)
为了测定气垫导轨上滑块的加速度,滑块上安装了宽度为3.0cm的遮光板,如图所示,滑块在牵引力作用下先后匀加速通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1=0.30s,通过第二个光电门的时间为△t2=0.10s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t=3.0s.则滑块的加速度是0.067m/s2(结果保留2位有效数字)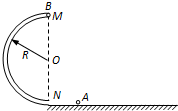 如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求
如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求