题目内容
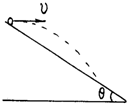 如图所示,将小球以EK0的初动能自倾角为θ的斜面顶端水平抛出,不计空气阻力,当它落到斜面上时,小球动能表达式为EKt=
如图所示,将小球以EK0的初动能自倾角为θ的斜面顶端水平抛出,不计空气阻力,当它落到斜面上时,小球动能表达式为EKt=(4tan2θ+1)EK0
(4tan2θ+1)EK0
.如果EK0=6J,θ=30°那么EKt14
14
J.分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住位移关系求出竖直分速度与水平分速度的关系,从而得出小球动能的大小.
解答:解:tanθ=
=
,所以vy=gt=2v0tanθ,则落到斜面上的动能Ekt=
mv2=
m(v02+vy2)=(4tan2θ+1)?
mv02=(4tan2θ+1)EK0.代入数据解得,Ekt=14J.
故答案为:(4tan2θ+1)EK0 14
| ||
| v0t |
| gt |
| 2v0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(4tan2θ+1)EK0 14
点评:解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式进行求解.

练习册系列答案
相关题目
(1)在“验证力的平行四边形定则”实验中,橡皮条一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一位置O点,以下操作正确的是( )
A.实验中必须记录弹簧秤拉力的方向
B.在实验中,弹簧秤必须保持与木板平行,读数时视线要正对弹簧秤的刻度
C.实验中,先将其中一个弹簧秤沿某一方向拉到最大量程,然后只需调节另一弹簧秤的拉力大小和方向,把橡皮条节点拉到O点
D.实验中,把橡皮条节点拉到O点时,两弹簧秤之间的夹角应取90°不变,以便于计算合力的大小
(2)一小球沿光滑斜面向下运动,用每隔0.1s曝光一次的频闪照相机拍摄下不同时刻小球的位置照片如图所示,选小球的五个连续位置A、B、C、D、E进行测量,测得距离s1、s2、s3、s4的数据如表格所示。
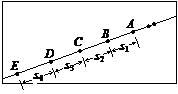 | |||||||||||
|

 某同学在做“利用单摆测重力加速度”的实验中,为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l和T的数值,再以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率K。则重力加速度g =
。(用K表示)用游标卡尺测小球半径, 一游标卡尺的主尺最小分度为1毫米,游标上有10个小等分间隔,现用此卡尺来测量工件的直径,如图所示。该小球的直径为_____________毫米。在该实验中,除秒表、铁架台、铁夹等器材外,还有以下器材供选用,请选出实验中还需要的器材 。(填器材前面的字母)
某同学在做“利用单摆测重力加速度”的实验中,为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l和T的数值,再以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率K。则重力加速度g =
。(用K表示)用游标卡尺测小球半径, 一游标卡尺的主尺最小分度为1毫米,游标上有10个小等分间隔,现用此卡尺来测量工件的直径,如图所示。该小球的直径为_____________毫米。在该实验中,除秒表、铁架台、铁夹等器材外,还有以下器材供选用,请选出实验中还需要的器材 。(填器材前面的字母)