题目内容
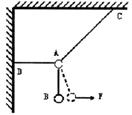
如图所示,两根轻细绳AB和AC的一端连接于竖直墙上,另一端系于一物体上,物体的质量为2 kg。现在物体上另施加一个方向与水平线成60°角的拉力F,若要使两绳都能伸直,则拉力F的取值范围如何?(取g=10 m/s2)
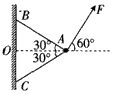
解:设AB的张力为F1,AC的张力为F2,建立如图所示的直角坐标系,对物体进行受力分析,根据平衡条件得:
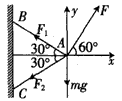
Fsin60°+F1sin30°=mg+F2sin30°
Fcos60°=F1cos30°+F2cos30°
当F较小时,绳AC中F2=0,即F和F1的合力与重力mg平衡
解得:Fmin=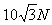
当F较大时,绳AB中张力F1=0,F和F2的合力与重力mg平衡
解得:Fmax=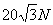
故拉力F的范围为: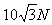 ≤F≤
≤F≤

Fsin60°+F1sin30°=mg+F2sin30°
Fcos60°=F1cos30°+F2cos30°
当F较小时,绳AC中F2=0,即F和F1的合力与重力mg平衡
解得:Fmin=
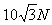
当F较大时,绳AB中张力F1=0,F和F2的合力与重力mg平衡
解得:Fmax=
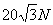
故拉力F的范围为:
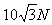 ≤F≤
≤F≤

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
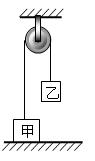
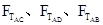 的变化情况是
的变化情况是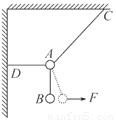
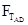 和
和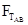 变大,
变大,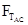 不变
不变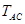 、
、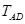 、
、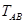 的变化情况是(
)
的变化情况是(
)