题目内容
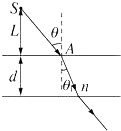
 如图所示.在折射率为n,厚度为d的玻璃平板上方的空气中有一点光源S,从点光源S发出的光线SA,以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,若沿此光线传播的光从光源到玻璃板上表面的传播时间与光在玻璃中传播的时间相等,则点光源S到玻璃板上表面的距离L应为多少?
如图所示.在折射率为n,厚度为d的玻璃平板上方的空气中有一点光源S,从点光源S发出的光线SA,以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,若沿此光线传播的光从光源到玻璃板上表面的传播时间与光在玻璃中传播的时间相等,则点光源S到玻璃板上表面的距离L应为多少?分析:根据数学知识分别用L表示光在空气中走过的距离和在玻璃中走过的距离.光在玻璃传播的速度为v=
,由折射定律求出折射角的正弦值.根据题意:光从光源到玻璃板上表面的传播时间与光在玻璃中传播的时间相等,列式求出L.
| c |
| n |
解答:解:光在空气中走过的距离为:s1=
,在玻璃中走过的距离为:s2=
.
设光在玻璃中传播的速度为v,则:v=
按题意有:t=
=
代入得:
=
解得:L=
?nd…①
由折射定律:n=
得:sinθ1=
所以:cosθ1=
=
…②
代入①有:L=
.
答:点光源S到玻璃板上表面的距离L为
.
| L |
| cosθ |
| d |
| cosθ1 |
设光在玻璃中传播的速度为v,则:v=
| c |
| n |
按题意有:t=
| s1 |
| c |
| s2 |
| v |
代入得:
| L |
| c?cosθ |
| d | ||
cosθ1?
|
解得:L=
| cosθ |
| cosθ1 |
由折射定律:n=
| sinθ |
| sinθ1 |
得:sinθ1=
| sinθ |
| n |
所以:cosθ1=
| 1-sin2θ1 |
| 1 |
| n |
| n2-sin2θ |
代入①有:L=
| n2dcosθ | ||
|
答:点光源S到玻璃板上表面的距离L为
| n2dcosθ | ||
|
点评:本题是折射定律、v=
及数学知识的综合应用,突破口是光在空气中和玻璃中的时间相等,将此文字语言变成数学表达式是关键.
| c |
| n |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目