题目内容
【题目】如图所示，质量为m的物体置于倾角为θ的固定斜面上，物体与斜面之间的动摩擦因数为μ，（0＜μ），先用平行于斜面的推力F1作用于物体上使其能沿斜面匀速上滑，若改用水平推力F2作用于物体上，也能使物体沿斜面匀速上滑，则（ ）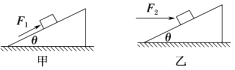
A.F1一定小于 F2
B.F1一定大于 F2
C.两次的推力之比 
为cosθ+μsinθ
D.两次的推力之比 为cosθ﹣μsinθ
【答案】A,D
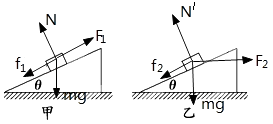
【解析】解：根据平衡条件建立方程：
对甲图 F1﹣mgsinθ﹣f1=0
N﹣mgcosθ=0
f1=μN
联立三个方程解得F1=mgsinθ+μmgcosθ
对乙图，将F2分解（或者正交分解）
平行斜面方向：F2cosθ﹣mgsinθ﹣f2=0
N′﹣Fsinθ﹣mgcosθ=0
f2=μN′
联立三个方程解得F2= 
；
AB、由于cosθ﹣μsinθ＜1，所以F2= ＞F1=mgsinθ+μmgcosθ，A符合题意、B不符合题意；
CD、两次的推力之比 
=cosθ﹣μsinθ，C不符合题意、D符合题意；
所以答案是：AD．
【考点精析】关于本题考查的滑动摩擦力和力的分解，需要了解滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解；求一个已知力的分力，叫做力的分解（力的分解与力的合成互为逆运算）；在实际问题中，通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究，在很多问题中都采用正交分解法才能得出正确答案．
阳光课堂课时优化作业系列答案
【题目】在“探究求合力的方法”实验中，现有木板、白纸、图钉、橡皮筋、细绳套和一把弹簧秤．
（1）为完成实验，某同学另找来一根弹簧，先测量其劲度系数，得到的实验数据如下表：
弹力F（N） | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
伸长量x（10﹣2 m） | 0.74 | 1.80 | 2.80 | 3.72 | 4.60 | 5.58 | 6.42 |
根据表中数据在如图1中作出F﹣x图象并求得该弹簧的劲度系数k=N/m；（保留两位有效数字）
（2）某次实验中，弹簧秤的指针位置如图2所示，其读数为N；同时利用（1）中结果获得弹簧上的弹力值为2.50N，请在图3中画出这两个共点力的合力F合；
（3）由图得到F合=N．（保留两位有效数字）
