题目内容
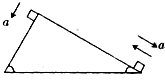如图所示，质量相同的A、B两个物块（两物体和斜面间的动摩擦因数不同）各沿一倾角分别为α=60°和β=30°的斜劈的两边运动，其中A沿斜面向下做加速度为a的匀加速运动，B沿斜面向上做加速度为a的匀减速运动．则关于斜劈和地面之间的摩擦力，以下说法正确的是（ ）分析：以A、B两个物块和斜劈整体为研究对象，分析受力情况，将两个物块的加速度分解为水平方向和竖直方向，根据牛顿第二定律确定地面对斜劈的摩擦力方向．
解答：解：以A、B两个物块和斜劈整体为研究对象，分析整体受到的外力情况如图，设地面对斜劈的摩擦力方向水平向右．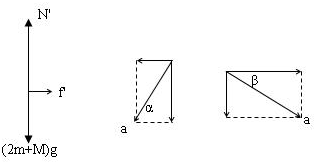
将两个物块的加速度分解为水平和竖直两个方向如图．
根据牛顿第二定律得：
水平方向：f=macosβ-macosα
由于β＜α，cosβ＞cosα，则有f＞0，说明地面对斜劈的摩擦力水平向右．
故选C
将两个物块的加速度分解为水平和竖直两个方向如图．根据牛顿第二定律得：
水平方向：f=macosβ-macosα
由于β＜α，cosβ＞cosα，则有f＞0，说明地面对斜劈的摩擦力水平向右．
故选C
点评：本题对三个加速度不同的物体运用整体法分析受力情况，将加速度进行分析是关键．
练习册系列答案
相关题目
如图所示，质量相同的A、B两球用细线悬挂于天花板上且静止不动．两球间是一个轻质弹簧，如果突然剪断悬线，则在剪断悬线瞬间（ ）
如图所示，质量相同的两个小球，分别用长l和2l的细线悬挂在天花板上．分别拉起小球使线伸直呈水平状态，然后轻轻释放，当小球到达最低位置时（ ）
如图所示，质量相同的木块A、B用轻弹簧相连，静止在光滑水平面上．弹簧处于自然状态．现用水平恒力F向右推A，则从开始推A到弹簧第一次被压缩到最短的过程中，下列说法中正确的是（ ）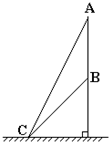
如图所示，质量相同的物体分别自斜面AC和BC的顶端由静止开始下滑，物体与斜面间的动摩擦因数都相同，物体滑到斜面底部C点时的动能分别为Ek1和Ek2，下滑过程中克服摩擦力所做的功分别为W1和W2，则（ ）
如图所示，质量相同的三个小球均可视为质点，处于同一水平面上．A球以初速度v0竖直上抛，B球以与水平面成θ角、大小也是v0的初速度斜向右上抛出，C球沿倾角为θ的足够长斜面以初速度v0上滑．上述运动过程中均不计空气阻力和一切摩擦，以下关于三个小球上升的最大高度的比较正确的是（ ）