题目内容
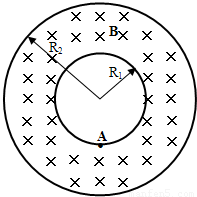
受控核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动使之束缚在某个区域内.现按下面的简化条件来讨论这个问题:如图所示的是一个截面为内径R1=0.6m、外径R2=1.2m的环状区域,区域内有垂直于截面向里的匀强磁场.已知氦核的荷质比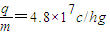 ,磁场的磁感应强度B=0.4T,不计带电粒子重力.
,磁场的磁感应强度B=0.4T,不计带电粒子重力.(1)把氢核聚变反应简化为4个氢核(
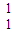 H)聚变成氦核(
H)聚变成氦核(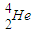 ),同时放出2个正电子(
),同时放出2个正电子(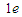 )和2个中微子(v),请写出该氢核聚变反应的方程,并给出一次核反应所释放能量的表达式.(氢核、氦核及电子的质量分别为mp、mα、me,光速为c)
)和2个中微子(v),请写出该氢核聚变反应的方程,并给出一次核反应所释放能量的表达式.(氢核、氦核及电子的质量分别为mp、mα、me,光速为c)(2)实践证明,氦核在磁场区域内沿垂直于磁场方向运动速度v的大小与它在磁场中运动的轨道半径r有关,试导出v与r的关系式;
(3)若氦核沿磁场区域的半径方向平行于截面从A点射入磁场,画出氦核在磁场中运动而不穿出外边界的最大圆轨道示意图;
(4)若氦核在平行于截面从A点沿各个方向射入磁场都不能穿出磁场外边界,求氦核的最大速度.
【答案】分析:(1)根据质量数、电荷数守恒写出氢核聚变反应的方程,根据质能方程求出次核反应所释放能量;
(2)由洛仑兹力充当向心力,利用牛顿第二定律可求导出粒了v与r的关系式;要使粒子均不能穿出磁场,由几何关系可得出粒子的最大半径,由半径公式可求得粒子的最大速度.
解答: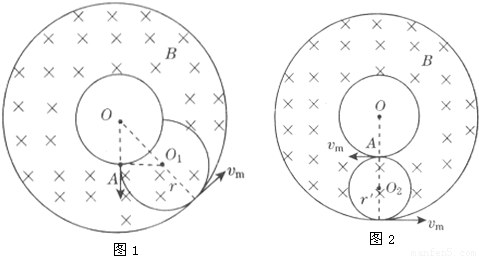 解:(l)根据质量数、电荷数守恒可知,氢核聚变反应的方程为:4
解:(l)根据质量数、电荷数守恒可知,氢核聚变反应的方程为:4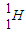 →
→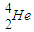 +2
+2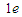 +2v
+2v
质量亏损为:△m=4mp-mα-2me
所以:△E=△mc2=(4mp-mα-2me)c2
(2)设氦核质量为m,电量为q,以速率v在磁感强度为B的匀强磁场中做半径为r的匀速圆周运动,
由洛仑兹力公式和牛顿定律得:
Bqv=m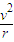
解得:v=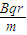
(3)所求轨迹示意图如图1所示(要与外圆相切)
(4)当氦核以vm的速度沿与内圆相切方向射入磁场且轨道与外圆相切时,则以vm速度沿各方向射人磁场区的氦核都不能穿出磁场外边界,如图2所示,由图可知:r′=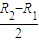
由①式可得:r=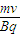
在速度为vm时不穿越磁场外界应满足的条件是: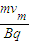 ≤r′
≤r′
代入数据可得:vm≤5.76×104m/s
答:(1)氢核聚变反应的方程为:4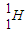 →
→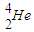 +2
+2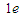 +2v,一次核反应所释放能量的表达式为(4mp-mα-2me)c2;
+2v,一次核反应所释放能量的表达式为(4mp-mα-2me)c2;
(2)v与r的关系式为v=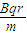 ;
;
(3)如图所示;
(4)氦核的最大速度为5.76×104m/s;
点评:带电粒子在有界磁场中的运动,要注意利用题目中给出的几何关系找出圆心及半径,即可由牛顿第二定律求出要求的量.
(2)由洛仑兹力充当向心力,利用牛顿第二定律可求导出粒了v与r的关系式;要使粒子均不能穿出磁场,由几何关系可得出粒子的最大半径,由半径公式可求得粒子的最大速度.
解答:
 解:(l)根据质量数、电荷数守恒可知,氢核聚变反应的方程为:4
解:(l)根据质量数、电荷数守恒可知,氢核聚变反应的方程为:4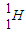 →
→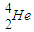 +2
+2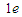 +2v
+2v 质量亏损为:△m=4mp-mα-2me
所以:△E=△mc2=(4mp-mα-2me)c2
(2)设氦核质量为m,电量为q,以速率v在磁感强度为B的匀强磁场中做半径为r的匀速圆周运动,
由洛仑兹力公式和牛顿定律得:
Bqv=m
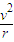
解得:v=
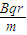
(3)所求轨迹示意图如图1所示(要与外圆相切)
(4)当氦核以vm的速度沿与内圆相切方向射入磁场且轨道与外圆相切时,则以vm速度沿各方向射人磁场区的氦核都不能穿出磁场外边界,如图2所示,由图可知:r′=
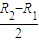
由①式可得:r=
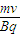
在速度为vm时不穿越磁场外界应满足的条件是:
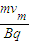 ≤r′
≤r′代入数据可得:vm≤5.76×104m/s
答:(1)氢核聚变反应的方程为:4
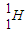 →
→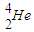 +2
+2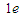 +2v,一次核反应所释放能量的表达式为(4mp-mα-2me)c2;
+2v,一次核反应所释放能量的表达式为(4mp-mα-2me)c2;(2)v与r的关系式为v=
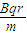 ;
;(3)如图所示;
(4)氦核的最大速度为5.76×104m/s;
点评:带电粒子在有界磁场中的运动,要注意利用题目中给出的几何关系找出圆心及半径,即可由牛顿第二定律求出要求的量.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
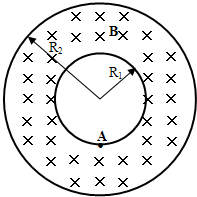 据有关资料介绍,受控核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动使之束缚在某个区域内.现按下面的简化条件来讨论这个问题:如图所示是一个截面为内径R1=0.6m、外径R2=1.2m的环状区域,区域内有垂直于截面向里的匀强磁场.已知氦核的荷质比
据有关资料介绍,受控核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动使之束缚在某个区域内.现按下面的简化条件来讨论这个问题:如图所示是一个截面为内径R1=0.6m、外径R2=1.2m的环状区域,区域内有垂直于截面向里的匀强磁场.已知氦核的荷质比 据有关资料介绍,受控核聚变装置中有极高的温度,因而带电粒子(核聚变的原料)将没有通常意义上的“容器”可装,而是由磁场来约束带电粒子运动使之束缚在某个区域内,右图是它的截面图,在外径为R2=1.2m、内径R1=0.6m的环状区域内有垂直于截面向里的匀强磁场,磁感强度B=0.4T,若氦核(其比荷q/m=4.8×107c/kg)在平行于截面的平面内从内圆上A点沿各个方向射入磁场都不能穿出磁场的外边界,求氦核的最大速度.(不计带电粒子的重力)
据有关资料介绍,受控核聚变装置中有极高的温度,因而带电粒子(核聚变的原料)将没有通常意义上的“容器”可装,而是由磁场来约束带电粒子运动使之束缚在某个区域内,右图是它的截面图,在外径为R2=1.2m、内径R1=0.6m的环状区域内有垂直于截面向里的匀强磁场,磁感强度B=0.4T,若氦核(其比荷q/m=4.8×107c/kg)在平行于截面的平面内从内圆上A点沿各个方向射入磁场都不能穿出磁场的外边界,求氦核的最大速度.(不计带电粒子的重力)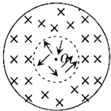 据有关资料介绍,受控核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动使之束缚在某个区域内(托卡马克装置).如图所示,环状匀强磁场围成中空区域,中空区域中的带电粒子只要速度不是很大,都不会穿出磁场的外边缘而被约束在该区域内,设环状磁场的内半径为R1=0.5m,外半径R2=1.0m,磁场的磁感应强度B=1.0T,若被束缚带电粒子的比荷为
据有关资料介绍,受控核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动使之束缚在某个区域内(托卡马克装置).如图所示,环状匀强磁场围成中空区域,中空区域中的带电粒子只要速度不是很大,都不会穿出磁场的外边缘而被约束在该区域内,设环状磁场的内半径为R1=0.5m,外半径R2=1.0m,磁场的磁感应强度B=1.0T,若被束缚带电粒子的比荷为