题目内容
15. 如图所示,用一根绝缘细线悬挂一个带电小球,小球质量为m,现加一水平向左的匀强电场,电场强度为E,平衡时细线与竖直方向成θ角.匀强电场区域足够大,则下列说法中正确的是( )
如图所示,用一根绝缘细线悬挂一个带电小球,小球质量为m,现加一水平向左的匀强电场,电场强度为E,平衡时细线与竖直方向成θ角.匀强电场区域足够大,则下列说法中正确的是( )| A. | 小球带正电 | B. | 小球所带电荷量为$\frac{mgcosθ}{E}$ | ||
| C. | 烧断丝线后,小球的加速度为$\frac{g}{cosθ}$ | D. | 烧断丝线后,小球将做曲线运动 |
分析 对小球受力分析,根据电场力方向判断小球的电性.根据共点力平衡求出电场力的大小,从而结合电场强度的定义式求出小球的电荷量.烧断丝线后,小球将做匀加速直线运动,由牛顿第二定律求加速度.
解答 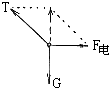 解:A、对小球受力分析,如图所示,小球所受的电场力水平向右,与场强方向相反,所以小球带负电.故A错误.
解:A、对小球受力分析,如图所示,小球所受的电场力水平向右,与场强方向相反,所以小球带负电.故A错误.
B、根据共点力平衡得 qE=mgtanθ,则 q=$\frac{mgtanθ}{E}$.故B错误.
CD、烧断丝线后,小球将沿原来细线的方向做匀加速直线运动,加速度为 a=$\frac{{F}_{合}}{m}$=$\frac{T}{mg}$=$\frac{\frac{mg}{cosθ}}{m}$=$\frac{g}{cosθ}$.故C正确,D错误.
故选:C
点评 解决本题的关键能够正确地受力分析,根据共点力平衡进行求解,要明确物体从静止开始受到恒力作用时将沿此恒力方向做匀加速直线运动.

练习册系列答案
相关题目
5. 如图所示,在竖直平面内,AB⊥CD且A、B、C、D位于同一半径为r的圆上,在C点有一固定点电荷,电荷量为-Q.现从A点将一质量为m、电荷量为-q的点电荷由静止释放,该点电荷沿光滑绝缘轨道ADB运动到D点时的速度大小为4$\sqrt{gr}$,规定电场中B点的电势为零,重力加速度为g.则在-Q形成的电场中( )
如图所示,在竖直平面内,AB⊥CD且A、B、C、D位于同一半径为r的圆上,在C点有一固定点电荷,电荷量为-Q.现从A点将一质量为m、电荷量为-q的点电荷由静止释放,该点电荷沿光滑绝缘轨道ADB运动到D点时的速度大小为4$\sqrt{gr}$,规定电场中B点的电势为零,重力加速度为g.则在-Q形成的电场中( )
 如图所示,在竖直平面内,AB⊥CD且A、B、C、D位于同一半径为r的圆上,在C点有一固定点电荷,电荷量为-Q.现从A点将一质量为m、电荷量为-q的点电荷由静止释放,该点电荷沿光滑绝缘轨道ADB运动到D点时的速度大小为4$\sqrt{gr}$,规定电场中B点的电势为零,重力加速度为g.则在-Q形成的电场中( )
如图所示,在竖直平面内,AB⊥CD且A、B、C、D位于同一半径为r的圆上,在C点有一固定点电荷,电荷量为-Q.现从A点将一质量为m、电荷量为-q的点电荷由静止释放,该点电荷沿光滑绝缘轨道ADB运动到D点时的速度大小为4$\sqrt{gr}$,规定电场中B点的电势为零,重力加速度为g.则在-Q形成的电场中( )| A. | A点的电势高于D点的电势 | |
| B. | O点的电场强度大小是A点的$\sqrt{2}$倍 | |
| C. | 点电荷-q在D点具有的电势能为7mgr | |
| D. | D点的电势为$\frac{7mgr}{q}$ |
6. 某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )
某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )
 某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )
某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )| A. | 物体在0一2s内做匀加速直线运动 | B. | 物体在第2秒末速度最大 | ||
| C. | 物体在第8秒末离出发点最远 | D. | 物体在第4s末速度方向发生改变 |
3. 如图所示,两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中,O为M、N连线中点,连线上a、b两点关于O点对称.两导线通有大小相等、方向相反的电流.已知长直导线周围产生的磁场的磁感应强度B=k$\frac{I}{r}$,式中k是常数,I是导线中的电流、r为点到导线的距离.一带负电的小球以初速度v0从a点出发沿连线运动到b点.关于上述过程,下列说法正确的是( )
如图所示,两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中,O为M、N连线中点,连线上a、b两点关于O点对称.两导线通有大小相等、方向相反的电流.已知长直导线周围产生的磁场的磁感应强度B=k$\frac{I}{r}$,式中k是常数,I是导线中的电流、r为点到导线的距离.一带负电的小球以初速度v0从a点出发沿连线运动到b点.关于上述过程,下列说法正确的是( )
 如图所示,两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中,O为M、N连线中点,连线上a、b两点关于O点对称.两导线通有大小相等、方向相反的电流.已知长直导线周围产生的磁场的磁感应强度B=k$\frac{I}{r}$,式中k是常数,I是导线中的电流、r为点到导线的距离.一带负电的小球以初速度v0从a点出发沿连线运动到b点.关于上述过程,下列说法正确的是( )
如图所示,两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中,O为M、N连线中点,连线上a、b两点关于O点对称.两导线通有大小相等、方向相反的电流.已知长直导线周围产生的磁场的磁感应强度B=k$\frac{I}{r}$,式中k是常数,I是导线中的电流、r为点到导线的距离.一带负电的小球以初速度v0从a点出发沿连线运动到b点.关于上述过程,下列说法正确的是( )| A. | 小球先做加速运动后做减速运动 | B. | 小球一直做匀速直线运动 | ||
| C. | 小球对桌面的压力先减小后增大 | D. | 小球对桌面的压力先增大后减小 |
10.在“测定直流电动机的效率”实验中,用如图(a)所示的电路测定一个额定电压为6V、额定功率为3W的直流电动机的机械效率.
(1)请根据图(a)完成图(b)中的实物图;

(2)实验中保持电动机两端电压U恒为6V,重物每次匀速上升的高度h均为1.5m,所测物理量及测量结果如下表所示:
计算电动机效率η的表达式为$η=\frac{mgh}{UIt}×100%$(用题目中的符号表示),第1次实验中电动机的工作效率为71.4%.(保留三位有效数字)
(3)在第5次实验中,电动机的输出功率是0;可估算出电动机线圈的电阻为2.4Ω.
(1)请根据图(a)完成图(b)中的实物图;

(2)实验中保持电动机两端电压U恒为6V,重物每次匀速上升的高度h均为1.5m,所测物理量及测量结果如下表所示:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电动机的电流I/A | 0.2 | 0.4 | 0.6 | 0.8 | 2.5 | 2.5 |
| 所提重物的重力Mg/N | 0.8 | 2.0 | 4.0 | 6.0 | 6.5 | 7.0 |
| 重物上升时间t/s | 1.4 | 1.65 | 2.1 | 2.7 | ∞ | ∞ |
(3)在第5次实验中,电动机的输出功率是0;可估算出电动机线圈的电阻为2.4Ω.
20.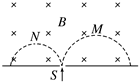 质量和电量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行半个圆周后穿出磁场,轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行半个圆周后穿出磁场,轨迹如图中虚线所示,下列表述正确的是( )
 质量和电量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行半个圆周后穿出磁场,轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行半个圆周后穿出磁场,轨迹如图中虚线所示,下列表述正确的是( )| A. | M带负电,N带正电 | |
| B. | M的速率大于N的速率 | |
| C. | M在磁场中运行时间大于N的运行时间 | |
| D. | M、N两粒子在洛伦兹力作用下分别向右、向左偏,故洛伦兹力对M、N都做了正功 |
7.关于原子核下列说法正确的是( )
| A. | 静止的原子核Ra226在匀强磁场中发生α衰变,沿着与磁场垂直的方向放出一个α粒子,此粒子的径迹与反冲核的径迹是两个相互外切的圆,α粒子轨迹半径较大 | |
| B. | 静止的原子核Th230在匀强磁场中发生β衰变,沿着与磁场垂直的方向放出一个电子,此粒子的径迹与反冲核的径迹是两个相互外切的圆,反冲核轨迹半径较大 | |
| C. | 一个U235核吸收一个中子后可能发生的反应是${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n,释放核能△E,则1kg U235反应释放能量为$\frac{1000}{235}△E$ | |
| D. | 重核裂变释放核能,生成的新核比结合能增大 |
18. 如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )| A. | t=$\frac{1}{600}$ s时,a、b两点间电压的瞬时值为5$\sqrt{2}$V | |
| B. | t=$\frac{1}{600}$ s时,电压表的读数为50$\sqrt{2}$V | |
| C. | 在1分钟内电阻R1上产生的热量为6000J | |
| D. | 当R2的温度升高时,电压表示数变大,电流表示数变大 |
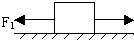 如图所示,水平面上有一重为40N的物体,受到向左F1=12N和向右F2=6N的水平力作用而保持静止.已知物体与水平面间的动摩擦因数μ=0.2,求:
如图所示,水平面上有一重为40N的物体,受到向左F1=12N和向右F2=6N的水平力作用而保持静止.已知物体与水平面间的动摩擦因数μ=0.2,求: