题目内容
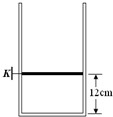 如图所示,足够长的圆柱形气缸竖直放置,其横截面积为1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底12cm,此时气缸内被封闭气体的压强1.5×105 Pa,温度为300K.外界大气压为1.0×105Pa,g=10m/s2.
如图所示,足够长的圆柱形气缸竖直放置,其横截面积为1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底12cm,此时气缸内被封闭气体的压强1.5×105 Pa,温度为300K.外界大气压为1.0×105Pa,g=10m/s2.(1)现对密闭气体加热,当温度升到400K,其压强多大?
(2)若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,气缸内气体的温度为360K,则这时活塞离缸底的距离为多少?
(3)保持气体温度为360K不变,让气缸和活塞一起在竖直方向作匀变速直线运动,为使活塞能停留在离缸底16cm处,则气缸和活塞应向什么方向作匀加速直线运动?加速度大小是多少?
分析:(1)直接根据理想气体状态方程列式求解;
(2)先根据平衡条件求解出封闭气体压强,然后根据理想气体状态方程列式求解;
(3)先根据理想气体状态方程列式求解封闭气体的气压,然后对活塞受力分析,求解加速度.
(2)先根据平衡条件求解出封闭气体压强,然后根据理想气体状态方程列式求解;
(3)先根据理想气体状态方程列式求解封闭气体的气压,然后对活塞受力分析,求解加速度.
解答:解:(1)等容变化:
=
,解得P2=
=
Pa=2.0×105Pa
(2)活塞受力平衡,故封闭气体压强为P3=P0+
=(1.0×105+
)Pa=1.2×105Pa
根据理想气体状态方程,有
=
,
∴L3=
=
cm=18cm
(3)等温变化 P3V3=P4V4,解得P4=
=
Pa=1.35×105Pa
应向上作匀加速直线运动,
对活塞,由牛顿第二定律:P4S-P0S-mg=ma
解得:a=
-g=
-10=7.5m/s2
答:(1)现对密闭气体加热,当温度升到400K,其压强为2.0×105Pa;
(2)这时活塞离缸底的距离为18cm;
(3)气缸和活塞应向上作匀加速直线运动,加速度大小是7.5m/s2.
| P1 |
| T1 |
| P2 |
| T2 |
| P1T2 |
| T1 |
| 1.5×105×400 |
| 300 |
(2)活塞受力平衡,故封闭气体压强为P3=P0+
| mg |
| S |
| 2×10 |
| 1×10-3 |
根据理想气体状态方程,有
| P2V2 |
| T2 |
| P3V3 |
| T3 |
∴L3=
| P2L2T3 |
| P3T2 |
| 2.0×105×12×360 |
| 1.2×105×400 |
(3)等温变化 P3V3=P4V4,解得P4=
| P3V3 |
| V4 |
| 1.2×105×18 |
| 16 |
应向上作匀加速直线运动,
对活塞,由牛顿第二定律:P4S-P0S-mg=ma
解得:a=
| (P4-P0)S |
| m |
| (1.35-1.0)×105×1×10-3 |
| 2 |
答:(1)现对密闭气体加热,当温度升到400K,其压强为2.0×105Pa;
(2)这时活塞离缸底的距离为18cm;
(3)气缸和活塞应向上作匀加速直线运动,加速度大小是7.5m/s2.
点评:本题关键是根据题意得到各个状态对应的压强、体积、温度中已知量,然后根据理想气体状态方程列式求解未知量.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 (2008?淮安模拟)如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直.在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计.整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中.当用水平向右的恒力F=
(2008?淮安模拟)如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直.在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计.整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中.当用水平向右的恒力F=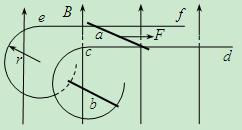
 mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求:
mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求:
 mg拉细杆
mg拉细杆 ,达到匀速运动时,杆b恰好静止在圆环上某处,试求:
,达到匀速运动时,杆b恰好静止在圆环上某处,试求: