题目内容
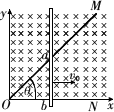
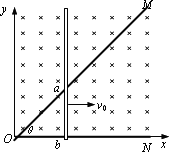
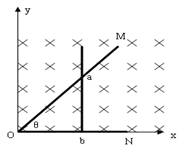
如图所示,顶角![]() =
=
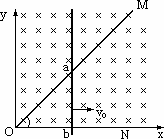
(1)t时刻流过导体棒的电流强度I和电流方向.
(2)导体棒作匀速直线运动时水平外力F的表达式.
(3)导体棒在0~t时间内产生的焦耳热Q.
(4)若在to时刻将外力F撤去,导体棒最终在导轨上静止时的坐标x.
答案:
解析:
解析:
|
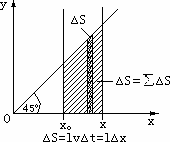
(1)0到t时间内,导体棒的位移x=v0t t时刻,导体棒的长度l=x 导体棒的电动势 E=Blv0 (4)撤去外力后,任意时刻t导体棒的坐标为x,速度为v,取很短时间Δt或很短距离Δx
解法一 在 t~t+Δt时间内,由动量定理得BIlΔt=mΔv 解法二 在 t~t+Δt时间内,由动能定理得 得 FΔx=mvΔv以下解法同解法二 |

练习册系列答案
相关题目