Question

用铁锤将一铁钉击入木块，设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时，能把铁钉击入木块内1 cm，问击第二次时，能击入多少深度？（设铁锤每次做功相等）

Answer 1

解析：本题考查对功概念的理解能力及理论联系实际抽象建立模型的能力，铁锤每次做功都用来克服铁钉阻力做的功，但摩擦阻力不是恒力，其大小与深度成正比，F=-f=kx.此题可以用平均力法解答，也可以用图象法解答.

答案：解法一：（平均力法）如下图，第一次击入深度为x₁,平均阻力,做功为W₁=.

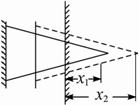
    第二次击入深度为x₁到x₂，平均阻力（x₂+x₁），位移为x₂-x₁，做功为

W₂=（x₂-x₁）=（）.

    两次做功相等：W₁=W₂

    解后有：x₂==1.41 cm

Δx=x₂-x₁=0.41 cm.

    解法二：（图象法）

    因为阻力F=kx,以F为纵坐标，F方向上的位移x为横坐标，作出Fx图象.如下图所示的曲线与x轴围成的面积的值等于F对铁钉做的功.

    由于两次做功相等，故有：

S₁=S₂（面积），即

（x₂+x₁）（x₂-x₁）

    所以Δx=x₂-x₁=0.41 cm.