题目内容
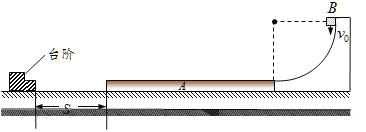
【题目】如图所示，质量为2m的木板A静止在光滑水平面上，其左端与固定台阶相距S，长木板的右端固定一半径为R光滑的四分之一圆弧，圆弧的下端与木板水平相切但不相连。质量为m的滑块B（可视为质点）以初速度
从圆弧的顶端沿圆弧下滑，当B到达最低点时，B从A右端的上表面水平滑入同时撤走圆弧．A与台阶碰撞无机械能损失，不计空气阻力，A、B之间动摩擦因数为μ，A足够长，B不会从A表面滑出；重力加速度为g．试分析下列问题：
（1）滑块B到圆弧底端时的速度大小v1；
（2）A与台阶只发生一次碰撞，求S满足的条件；
（3）S在满足（2）条件下，讨论A与台阶碰撞前瞬间B的速度。
【答案】（1）
（2）
（3）
或
【解析】
试题分析: （1）滑块B从释放到最低点，机械能守恒，取水平面为零势面，由机械能守恒定律得：
①
由①解得： ②
（2）设A与台阶碰撞前瞬间，A、B的速度分别为vA和vB，由动量守恒定律得：
③
若A与台阶只碰撞一次，碰撞后必须满足：
④
对A应用动能定理：
⑤
联立③④⑤解得： ⑥
即A与台阶只能碰撞一次的条件是：
（3）设S=
时，A左端到台阶板前瞬间，A、B恰好达到共同速度
，由动量守定律得：
⑦
对A应用动能定理：
⑧
联立⑦⑧得：
讨论： （i）当
即
时，AB共速后A才与挡板碰撞．
由⑦式可得A与台阶碰撞前瞬间的A、B的共同速度为：
即A与台阶碰撞前瞬间B的速度为：
（ii）当
即
时，AB共速前A就与台阶碰撞，
对A应用动能定理有：
由上式解得A与台阶碰撞前瞬间的速度：
设此时B的速度为
，由动量守恒定律得：
由上式解得：
练习册系列答案
相关题目
