题目内容
9.假设一小型宇宙飞船沿人造地球卫星的轨道在高空做匀速圆周运动,运动周期为T,如果飞船沿与其速度相反的方向抛出一个物体A(假设物体速度可以从较小值到足够大值任意取一个值),以后的运动可能是( )| A. | 物体A与飞船运动周期都等于T | |
| B. | 物体A的运动周期等于T,而飞船的运动周期大于T | |
| C. | 物体A竖直下落,飞船做椭圆轨道运动 | |
| D. | 位移A和飞船的运动周期都大于T |
分析 整个过程中系统动量守恒,而抛出后A的速度方向有几种可能,根据抛出后A的速度的大小和方向结合向心力的知识判断A物体的运动情况.
解答 解:万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,
解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$;
飞船沿与其速度相反的方向发射一个物体A的过程,飞船与A组成的系统动量守恒,
因为物体A是沿飞船向后抛出,由动量守恒定律可知,飞船的动量一定增大,飞船的速度增大,动能增大,将做离心运动,上升到高轨道,飞船的轨道半径r飞船变大,飞船不可能在原轨道运动,由T=2π$\sqrt{\frac{{r}^{3}}{GM}}$可知,飞船的周期T变大,故A错误.
而抛出后物体的速度方向有几种可能:
①若抛出后物体的速度方向与飞船方向相同,则物体A的速度减小,将做近心运动,rA变小,由T=2π$\sqrt{\frac{{r}^{3}}{GM}}$可知,A的周期变小,小于T;
②若抛出后物体的速度为零,则A会在万有引力的作用下竖直下落.
③若物体的速度方向与飞船方向相反,其大小可能等于飞船原来的速度,此时仍将在原轨道运行,rA不变,由由T=2π$\sqrt{\frac{{r}^{3}}{GM}}$可知可知,A的周期不变,等于T;
A的速度也可能大于飞船原来的速度,此时也将上升到高轨道运动,rA变大,由由T=2π$\sqrt{\frac{{r}^{3}}{GM}}$可知,A的周期变大,大于T;
由以上分析可知,BCD正确,A错误;
故选:BCD.
点评 本题考查了万有引力定律的应用;根据动量守恒分析物体速度的大小和方向的可能性.当万有引力刚好提供卫星所需向心力时 卫星正好可以做匀速圆周运动,
1.若是供大于需 则卫星做逐渐靠近圆心的运动;2.若是供小于需 则卫星做逐渐远离圆心的运动.

 名校课堂系列答案
名校课堂系列答案| A. | 加速度的大小在数值上等于单位时间内速度的改变量,因此每秒钟速率的增量在数值上等于加速度的大小 | |
| B. | 枪膛中子弹的加速度约为105m/s2射出的速度可达1000m/s左右,所以加速度大,速度变化就大 | |
| C. | 汽车的加速性能是反映汽车质量优劣的一项重要指标,因为加速度大,汽车速度变化快,启动性能好 | |
| D. | 物体加速度为正值时,物体速度就增大,物体加速度为负值时,物体速度就减小 |
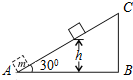 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 克服摩擦力做功0.5mgh | ||
| C. | 动能损失了2mgh | D. | 机械能损失了mgh |
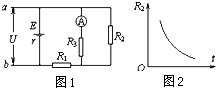 如图1所示是一火警报警器的部分电路示意图,其中R2为半导体热敏材料制成的传感器,其电阻R2随温度t变化的图线如图2所示.电流表为值班室的显示器,a、b之间接报警器.当传感器R2所在处出现火情时,显示器的电流I和报警器两端的电压U的变化情况是( )
如图1所示是一火警报警器的部分电路示意图,其中R2为半导体热敏材料制成的传感器,其电阻R2随温度t变化的图线如图2所示.电流表为值班室的显示器,a、b之间接报警器.当传感器R2所在处出现火情时,显示器的电流I和报警器两端的电压U的变化情况是( )| A. | I 变大,U 变大 | B. | I 变大,U 变小 | C. | I 变小,U 变大 | D. | I 变小,U 变小 |
| A. | 磁感线是闭合曲线 | |
| B. | 磁感线密处磁场弱 | |
| C. | 小磁针静止时S极所指方向为该处磁场的方向 | |
| D. | 地球北极的地磁场方向竖直向上 |

 如图是F1赛车测试场地数据中的运动情景,试求:
如图是F1赛车测试场地数据中的运动情景,试求: