题目内容
4.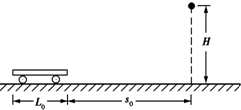 如图所示,质量为m的小车静止在光滑的水平地面上,车长为L.现给小车施加一个水平向右的恒力F使小车向右匀加速运动,与此同时在小车的正前方s0处的正上方H高处有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),试求:
如图所示,质量为m的小车静止在光滑的水平地面上,车长为L.现给小车施加一个水平向右的恒力F使小车向右匀加速运动,与此同时在小车的正前方s0处的正上方H高处有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),试求:(1)小球下落的时间;
(2)要使小球落到小车上,小车高度忽略不计,恒力F的取值范围.
分析 小球自由下落的高度一定,则下落的时间一定,小球落在小车上,则在这段时间内的位移大于s0,小于(L+s0),根据匀变速直线运动的位移时间公式求出小车加速度的范围.从而得出恒力F的取值范围.
解答 解:(1)由于小球做自由落体运动,所以有:$H=\frac{1}{2}g{t^2}$,
即 $t=\sqrt{\frac{2H}{g}}$.
(2)设当小球刚好落到小车的前端时小车的加速度为 $a=\frac{F_1}{m}$,
小车运动的位移$s={s_0}=\frac{1}{2}a{t^2}$
所以${F_1}=\frac{{2m{s_0}}}{t^2}=\frac{{mg{s_0}}}{H}$.
设当小球刚好落到小车的末端时,小车的加速度$a'=\frac{F_2}{m}$,
小车运动的位移$s={s_0}+{L_0}=\frac{1}{2}a'{t^2}$,所以${F_2}=\frac{{2m({s_0}+{L_0})}}{t^2}=\frac{{mg({s_0}+{L_0})}}{H}$.
要使小球落到小车上,恒力F的取值范围为$\frac{{mg{s_0}}}{H}$≤F≤$\frac{{mg({s_0}+{L_0})}}{H}$.
答:(1)小球下落的时间为$\sqrt{\frac{2H}{g}}$;
(2)要使小球落到小车上,小车高度忽略不计,恒力F的取值范围$\frac{{mg{s_0}}}{H}$≤F≤$\frac{{mg({s_0}+{L_0})}}{H}$.
点评 解决本题的关键抓住小球下落的时间和小车运动的时间相等,运用匀变速直线运动位移时间公式求加速度的范围.

练习册系列答案
相关题目
14.下述说法中正确的是( )
| A. | 力越大,位移越大,做功就越多 | |
| B. | 力很大,位移很大,这个力的功可能为零 | |
| C. | 力的方向与运动方向相同时,功就等于这个力与位移大小的乘积 | |
| D. | 力很大,位移很大,这个力做的功一定很大 |
12.关于质点,下列说法正确的是( )
| A. | 质点一定代表一个小球 | |
| B. | 质量很大的物体不能用质点表示 | |
| C. | 无论大物体还是小物体,在机械运动中一律看做质点 | |
| D. | 研究地球绕太阳的公转时,可以把地球视作质点 |
19.在自由落体运动中,第一个2s、第二个2s和第5s内的位移之比为( )
| A. | 1:3:5 | B. | 2:6:5 | C. | 2:8:7 | D. | 4:12:9 |
13. 将一只苹果(可看成质点)斜向上抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹.若不计空气阻力的影响,以下说法中正确的是( )
将一只苹果(可看成质点)斜向上抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹.若不计空气阻力的影响,以下说法中正确的是( )
 将一只苹果(可看成质点)斜向上抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹.若不计空气阻力的影响,以下说法中正确的是( )
将一只苹果(可看成质点)斜向上抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹.若不计空气阻力的影响,以下说法中正确的是( )| A. | 苹果通过第1个窗户所用的时间最长 | |
| B. | 苹果通过第3个窗户的平均速度最大 | |
| C. | 苹果通过第1个窗户重力所做的功最多 | |
| D. | 苹果通过第3个窗户克服重力做功的平均功率最小 |
 如图所示,有两颗人造地球卫星围绕地球运动,它们运行的轨道可能是①③,所有的卫星轨道平面都圆心与地心重合.
如图所示,有两颗人造地球卫星围绕地球运动,它们运行的轨道可能是①③,所有的卫星轨道平面都圆心与地心重合.
 如图所示,光滑金属球的重量G=40N,它的左侧紧靠竖直的墙壁,右侧置于倾角θ=37°的斜面体上.已知斜面体置于水平地面上保持静止状态,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑金属球的重量G=40N,它的左侧紧靠竖直的墙壁,右侧置于倾角θ=37°的斜面体上.已知斜面体置于水平地面上保持静止状态,sin37°=0.6,cos37°=0.8.求: 质量为m的小环A穿在半径为R=0.5m的光滑大环上,大环绕竖直轴转动后A球与大环的圆心的连线与竖直轴成60°的夹角时,大环匀速转动.A球就在此位置和大环相对静止.
质量为m的小环A穿在半径为R=0.5m的光滑大环上,大环绕竖直轴转动后A球与大环的圆心的连线与竖直轴成60°的夹角时,大环匀速转动.A球就在此位置和大环相对静止.