题目内容
如图,在x轴上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外;在x轴下方存在匀强电场,电场方向与xOy平面平行,且与x轴成 夹角。一质量为m、电荷量为q(q>0)的粒子以初速度v0从y轴上的P点沿y轴正方向射出,一段时间后进入电场,进入电场时的速度方向与电场方向相反;又经过一段时间T0,磁场的方向变为垂直于纸面向里,大小不变。不计重力。
夹角。一质量为m、电荷量为q(q>0)的粒子以初速度v0从y轴上的P点沿y轴正方向射出,一段时间后进入电场,进入电场时的速度方向与电场方向相反;又经过一段时间T0,磁场的方向变为垂直于纸面向里,大小不变。不计重力。
(1)求粒子从P点出发至第一次到达x轴时所需时间;
(2)若要使粒子能够回到P点,求电场强度的最大值。
(1) (2)
(2)
解析试题分析:(1)带电粒子在磁场中做圆周运动,设运动半径为R,运动周期为T,根据洛仑兹力公式及圆周运动规律,有
 1
1 2
2
依题意,粒子第一次到达x轴时,运动转过的角度为 ,所需时间
,所需时间 为
为 3
3
联立123式得 4
4
(2)粒子进入电场后,先做匀减速运动,直到速度减小到0;然后沿原路返回做匀加速运动,到达x轴时速度大小仍为 。设粒子在电场中运动的总时间为
。设粒子在电场中运动的总时间为 ,加速度大小为a,电场强度大小为E,有
,加速度大小为a,电场强度大小为E,有 5
5 6
6
联立56式得 7
7
根据题意,要使粒子能够回到P点,必须满足 8
8
联立78式得,电场强度的最大值为
考点:带电粒子在电磁场中的运动
【方法技巧】解决带电粒子在电磁场中的运动问题时,要深入细致的理解题意,并根据题干描述,找出关键位置,画出粒子的运动草图,灵活运用各种几何关系来求解。

练习册系列答案
相关题目

 。沿东西方向放置长为20m的直导线,通有由西向东30A的电流,该导线受地磁场作用力的大小为_____ ______N,方向为________ ___(填“竖直向下”或“竖直向上”)。
。沿东西方向放置长为20m的直导线,通有由西向东30A的电流,该导线受地磁场作用力的大小为_____ ______N,方向为________ ___(填“竖直向下”或“竖直向上”)。
 =1×108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上.不计粒子重力.求:
=1×108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上.不计粒子重力.求: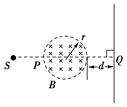
 的圆将
的圆将 平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于
平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于 的位置。一束质量为
的位置。一束质量为 、电荷量为q、速度为
、电荷量为q、速度为 的带正电粒子从坐标为(
的带正电粒子从坐标为( ,0)的A点沿x轴正方向射入区域Ⅰ,粒子全部垂直打在荧光屏上坐标为(0,-2R)的
,0)的A点沿x轴正方向射入区域Ⅰ,粒子全部垂直打在荧光屏上坐标为(0,-2R)的 点。若区域Ⅱ中加上平行于x轴的匀强电场,从A点沿x轴正方向以速度2
点。若区域Ⅱ中加上平行于x轴的匀强电场,从A点沿x轴正方向以速度2



 试推导出电子比荷
试推导出电子比荷 的表达式;
的表达式;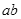 质量为
质量为 ,电阻为
,电阻为 ,放在与水平面夹角为
,放在与水平面夹角为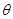 的倾斜金属导轨上,导轨间距为
的倾斜金属导轨上,导轨间距为 ,电阻不计,系统处在竖直向上的匀强磁场中,磁感应强度为
,电阻不计,系统处在竖直向上的匀强磁场中,磁感应强度为 ,电源的内阻不计,重力加速度为
,电源的内阻不计,重力加速度为 。求:
。求:
 为多大能使导体杆静止在导轨上;
为多大能使导体杆静止在导轨上;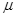 ,且不通电时导体杆不能静止在导轨上,要使杆在导轨上匀速下滑,电源的电动势
,且不通电时导体杆不能静止在导轨上,要使杆在导轨上匀速下滑,电源的电动势 应为多大。
应为多大。