题目内容
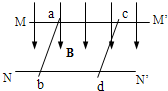 (2010?红桥区二模)如图所示,两条无限长且光滑的平行金属导轨MM′.NN′的电阻为零,相距l=0.4m,水平放置在方向竖直向下、磁感应强度B=0.5T的匀强磁场中,ab,cd两金属棒长度与导轨宽度相同,电阻均为R=0.5Ω,垂直地跨放在导轨上,ab的质最为m1=0.4kg,cd的质量为m2=0.1kg,开始将cd棒锁定在导轨上,给ab棒一个向左的瞬时冲量,以初速度v1=5m/s开始滑动,当速度降为v0=10m/s时,将对cd棒的锁定解除.
(2010?红桥区二模)如图所示,两条无限长且光滑的平行金属导轨MM′.NN′的电阻为零,相距l=0.4m,水平放置在方向竖直向下、磁感应强度B=0.5T的匀强磁场中,ab,cd两金属棒长度与导轨宽度相同,电阻均为R=0.5Ω,垂直地跨放在导轨上,ab的质最为m1=0.4kg,cd的质量为m2=0.1kg,开始将cd棒锁定在导轨上,给ab棒一个向左的瞬时冲量,以初速度v1=5m/s开始滑动,当速度降为v0=10m/s时,将对cd棒的锁定解除.(1)在解除对cd棒的锁定前,电路中一共产生了多少焦耳热?
(2)在cd刚开始运动时,cd棒的加速度多大?
(3)cd棒能获得的最大速度是多大?
分析:(1)对cd棒由能量守恒定律,即可求解;
(2)根据法拉第电磁感应定律,与闭合电路欧姆定律及牛顿第二定律相结合,即可求解;
(3)对系统在水平方向运用动量守恒定律,从而即可求解.
(2)根据法拉第电磁感应定律,与闭合电路欧姆定律及牛顿第二定律相结合,即可求解;
(3)对系统在水平方向运用动量守恒定律,从而即可求解.
解答:解:
(1)在解除对cd棒的锁定前,电路中产生的焦耳热为
Q=
m1
-
m1
解得:Q=15J
(2)在cd刚开始运动时,ab棒产生的感应电动势为
E=Blv1=0.5×0.4×5V=1V
回路中的感应电流I=
=
A=1A
cd棒受到的安培力为F=BIl=0.5×1×0.4N=0.2N
cd棒的加速度大小为a=
=
m/s2=2m/s2
(3)ab棒cd棒组成的系统水平方向动量守恒,cd棒的最大速度为v,
则有,动量守恒定律:
m1v1=(m1+m2)v
解得:v=4m/s
答:(1)在解除对cd棒的锁定前,电路中一共产生了15J焦耳热;
(2)在cd刚开始运动时,cd棒的加速度2m/s2;
(3)cd棒能获得的最大速度是4m/s.
(1)在解除对cd棒的锁定前,电路中产生的焦耳热为
Q=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
解得:Q=15J
(2)在cd刚开始运动时,ab棒产生的感应电动势为
E=Blv1=0.5×0.4×5V=1V
回路中的感应电流I=
| E |
| 2R |
| 1 |
| 2×0.5 |
cd棒受到的安培力为F=BIl=0.5×1×0.4N=0.2N
cd棒的加速度大小为a=
| F |
| m |
| 0.2 |
| 0.1 |
(3)ab棒cd棒组成的系统水平方向动量守恒,cd棒的最大速度为v,
则有,动量守恒定律:
m1v1=(m1+m2)v
解得:v=4m/s
答:(1)在解除对cd棒的锁定前,电路中一共产生了15J焦耳热;
(2)在cd刚开始运动时,cd棒的加速度2m/s2;
(3)cd棒能获得的最大速度是4m/s.
点评:考查能量守恒定律、法拉第电磁感应定律、闭合电路欧姆定律、牛顿第二定律、动量守恒定律等规律的应用,注意动量守恒定律事先做出守恒的判定,此处强调水平方向守恒.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目

 (2010?红桥区二模)我国成功发射的“神舟五号”载人飞船,经过21h的太空飞行,返回舱于次日安全着陆.已知飞船在太空中运行的轨道是一个椭圆,椭圆的一个焦点是地球的球心,如图所示,飞船在飞行中是无动力飞行,只受到地球的万有引力作用,在飞船从轨道的A点沿箭头方向运行到B点的过程中(不考虑地球的运动),以下说法正确的是( )
(2010?红桥区二模)我国成功发射的“神舟五号”载人飞船,经过21h的太空飞行,返回舱于次日安全着陆.已知飞船在太空中运行的轨道是一个椭圆,椭圆的一个焦点是地球的球心,如图所示,飞船在飞行中是无动力飞行,只受到地球的万有引力作用,在飞船从轨道的A点沿箭头方向运行到B点的过程中(不考虑地球的运动),以下说法正确的是( ) (2010?红桥区二模)如图所示,半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内,轨道的B端切线水平,且距水平地面高度为h=1.25m.现将一质量m=0.2kg的小滑块(可视为质点)从A点由静止释放,小滑块沿圆弧轨道运动至B点以v=5m/s的速度水平抛出,
(2010?红桥区二模)如图所示,半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内,轨道的B端切线水平,且距水平地面高度为h=1.25m.现将一质量m=0.2kg的小滑块(可视为质点)从A点由静止释放,小滑块沿圆弧轨道运动至B点以v=5m/s的速度水平抛出, (2010?红桥区二模)如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上,甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动,则( )
(2010?红桥区二模)如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上,甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动,则( )