Question

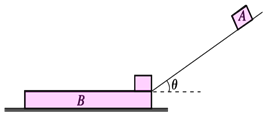
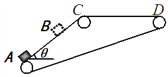
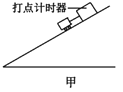
【题目】如图，AB为光滑斜面，BC为粗糙斜面，两斜面的倾角均为37°，且斜面底部B处平滑连接，质量为m＝2kg的物体从高为h＝1.25m的A处由静止开始沿斜面下滑，运动到BC斜面上最终停止在C处。设物体与BC斜面间的最大静摩擦力等于滑动摩擦力，物体与BC斜面的动摩擦因数为μ＝0.75，sin37°＝0.6，cos37°＝0.8，取g＝10m/s2。求：

（1）物体在B处的速度大小vB；

（2）物体在BC斜面上的运动时间t；

（3）若BC斜面的倾角可在0~60°范围内变化，请分析并说明物体从A处释放后在BC斜面上可能的运动情况。

Answer 1

【答案】（1）5m/s（2）s（3）见解析；

【解析】（1）物体沿AB斜面运动时的受力如图所示；

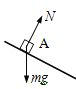
因为只有重力做功，此过程中机械能守恒。

mghA＝mvB2

代入数据，得vB＝5m/s

（2）物体在BC斜面上运动时的受力如图所示，

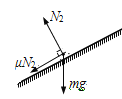
根据牛顿第二定律，mgsin37°＋μN2＝ma2

N＝mgcos37°

数据代入上述两式，得a2＝12m/s2

物体受恒力作用，做匀减速运动，

（3）设BC斜面倾角为θ时，物体恰好静止，受力如图所示，

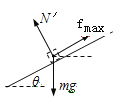
根据平衡条件，fmax＝μmgcosθ＝mgsinθ，得tgθ＝0.75，θ＝37°

当θ≤37°时，fmax＞mgsinθ，物体在BC斜面上做匀减速运动，速度减为零后保持静止。

当θ＞37°时，fmax＜mgsinθ，物体在BC斜面上做匀减速运动，速度减为零后沿BC斜面向下做匀加速运动，随后运动到AB斜面，此后反复在两斜面间运动若干次，最终静止在B点。