题目内容
15. 如图所示,斜面直轨道是粗粮的,大、小圆轨道光滑且均与斜面直轨道相切,切点分别为C、B,圆形轨道的出人口错开,大、小圆轨道的最高点跟斜面的最高点在同一水平线上,斜面直轨道的倾角为60°.今有一质量为m的小球自A以初速度v0沿斜面滑下,运动到B后进入小圆形轨道,接着再沿斜面下滑进人大圆形轨道运动,小球与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,求:
如图所示,斜面直轨道是粗粮的,大、小圆轨道光滑且均与斜面直轨道相切,切点分别为C、B,圆形轨道的出人口错开,大、小圆轨道的最高点跟斜面的最高点在同一水平线上,斜面直轨道的倾角为60°.今有一质量为m的小球自A以初速度v0沿斜面滑下,运动到B后进入小圆形轨道,接着再沿斜面下滑进人大圆形轨道运动,小球与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,求:(1)若小球恰能到达大圆轨道的最高点,则v0应满足什么条件?
(2)在v0满足(1)的前提条件下,求小球在小圆轨道的最高点时对轨道的压力.
分析 根据几何关系求出大圆的半径,根据牛顿第二定律求出最高点的临界速度,通过动能定理求出初速度应满足的条件.
根据动能定理求出小球在小圆轨道最高点的速度,从而根据牛顿第二定律求出弹力的大小
解答 解:(1)设C处圆形轨道的半径为R′,
则由几何关系可知,A到B处圆轨圆心的距离为$A{O}_{1}=\frac{R}{sin30°}$,
而且$\frac{R′}{3R+R′}=sin30°$,
解得R′=3R,
斜面轨道AB=$Rcot30°=\sqrt{3}R={s}_{1}$,①
$AC=3Rcot30°=3\sqrt{3}R={s}_{2}$ ②
小球由A到C处圆形轨道的最高点的过程由动能定理有:
$-μmgcos60°•{s}_{2}=\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{0}^{2}$ ③
由于小球恰能到达C处圆轨道的最高点,故v=$\sqrt{gR′}$. ④
联立①②③④解得${v}_{0}=\sqrt{6gR}$. ⑤
(2)设小球到达B处圆形轨道的最高点的速度为v1,
小球由A到B处圆形轨道最高点的过程,由动能定理有:
$-μmgcos60°•{s}_{1}=\frac{1}{2}{mv}_{1}^{2}-\frac{1}{2}{mv}_{0}^{2}$ ⑥
设小球在B处圆形轨道最高点受轨道压力为FN,
由牛顿第二定律可知,${F}_{N}+mg=\frac{{mv}_{1}^{2}}{R}$ ⑦
联立①⑤⑥⑦解得FN=4mg.
答:(1)小球恰能到达大圆轨道的最高点,则v0应满足大于等于$\sqrt{6\sqrt{R}}$;
(2)小球在小圆轨道的最高点时受到的轨道的弹力大小是4mg
点评 本题考查了圆周运动和动能定理、牛顿第二定律的综合,知道圆周运动向心力的来源是解决本题的关键,本题对数学几何能力的要求较高,需加强训练

| A. | 处于静电平衡的导体,内部的电场强度和电势均为零 | |
| B. | 避雷针避雷是利用尖端放电中和空气中的异种电荷 | |
| C. | 电场线跟等势面垂直,且沿着电场线方向电势逐渐降低 | |
| D. | 电场和磁场都是真实存在的物质 |
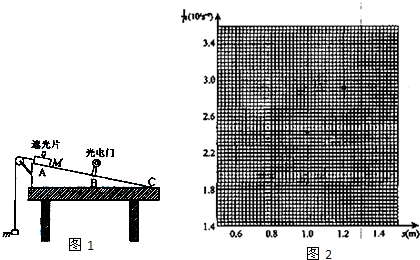
完成下列填空和作图;
(1)若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片与砝码组成的系统重力势能的减小量可表示为Mg$\frac{h}{d}$s-mgs.动能的增加量可表示为$\frac{1}{2}$(m+M)$\frac{{b}^{2}}{{t}^{2}}$.若在运动过程中机械能守恒,$\frac{1}{{t}^{2}}$与s的关系式为$\frac{1}{{t}^{2}}$=$\frac{2(hM-dm)g}{(M+m)d{b}^{2}}$s.
(2)多次改变光电门的位置,每次均令滑块自同一点(A点)下滑,测量相应的s与t值,结果如表所示:
| 1 | 2 | 3 | 4 | 5 | |
| S(m) | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| T(m/s) | 8.22 | 7.17 | 6.44 | 5.85 | 5.43 |
| 1/t2(104s-2) | 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |
由测得的h、d、b、M和m数值可以计算出$\frac{1}{{t}^{2}}$-s直线的斜率k0,将k和k0进行比较,若其差值在实验允许的范围内,则可认为此实验验证了机械能守恒定律.
 跳伞运动员从离地500m的直升机上跳下,先做初速度为零的匀加速直线运动,经过2s拉开绳索开启降落伞,做变速直线运动,14s后做匀速直线运动,如图所示是整个跳伞过程的v-t图象,试根据图象求:
跳伞运动员从离地500m的直升机上跳下,先做初速度为零的匀加速直线运动,经过2s拉开绳索开启降落伞,做变速直线运动,14s后做匀速直线运动,如图所示是整个跳伞过程的v-t图象,试根据图象求: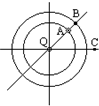 如图所示,在点电荷Q形成的电场中有A、B、C三点,若Q为负电荷,则A点场强最大,则A点电势最低.
如图所示,在点电荷Q形成的电场中有A、B、C三点,若Q为负电荷,则A点场强最大,则A点电势最低.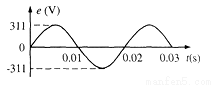

 2008年9月25日21点10分,我国“神舟”七号载人飞船发射成功,飞船绕地球45.5圈后,于9月28日17点25分安全返回,历时68小时15分.若把“神舟”七号载人飞船的绕地运行看作是在同一轨道上的匀速圆周运动,已知地球半径为R,地球表面重力加速度为g.
2008年9月25日21点10分,我国“神舟”七号载人飞船发射成功,飞船绕地球45.5圈后,于9月28日17点25分安全返回,历时68小时15分.若把“神舟”七号载人飞船的绕地运行看作是在同一轨道上的匀速圆周运动,已知地球半径为R,地球表面重力加速度为g.