题目内容
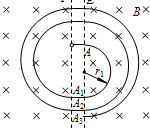 (2011?海淀区一模)如图所示,相距为d的狭缝P、Q间存在着方向始终与P、Q平面垂直、电场强度大小为E的匀强电场,且电场的方向按一定规律分时段变化.狭缝两侧均有磁感强度大小为B、方向垂直纸面向里的匀强磁场,且磁场区域足够大.某时刻从P平面处由静止释放一个质量为m、带电荷为q的带负电粒子(不计重力),粒子被加速后由A点进入Q平面右侧磁场区,以半径r1做圆运动,此时电场的方向已经反向,当粒子由A1点自右向左通过Q平面后,使粒子再次被加速进入P平面左侧磁场区做圆运动,此时电场又已经反向,粒子经半个圆周后通过P平面进入PQ狭缝又被加速,….以后粒子每次通过PQ间都被加速.设粒子自右向左穿过Q平面的位置分别是A1、A2、A3、…An…,求:
(2011?海淀区一模)如图所示,相距为d的狭缝P、Q间存在着方向始终与P、Q平面垂直、电场强度大小为E的匀强电场,且电场的方向按一定规律分时段变化.狭缝两侧均有磁感强度大小为B、方向垂直纸面向里的匀强磁场,且磁场区域足够大.某时刻从P平面处由静止释放一个质量为m、带电荷为q的带负电粒子(不计重力),粒子被加速后由A点进入Q平面右侧磁场区,以半径r1做圆运动,此时电场的方向已经反向,当粒子由A1点自右向左通过Q平面后,使粒子再次被加速进入P平面左侧磁场区做圆运动,此时电场又已经反向,粒子经半个圆周后通过P平面进入PQ狭缝又被加速,….以后粒子每次通过PQ间都被加速.设粒子自右向左穿过Q平面的位置分别是A1、A2、A3、…An…,求:(1)粒子第一次在Q右侧磁场区做圆运动的半径r1的大小;
(2)粒子第一次和第二次通过Q平面的位置A1和A2之间的距离;
(3)设An与An+1间的距离小于r1/3,则n值为多大.
分析:带电粒子被电场加速,可以使用动能定理求出它的速度,在磁场中洛伦兹力提供向心力,可以求出粒子的半径.
解答:解:(1)带电粒子被电场加速,由动能定理:qEd=
m
洛伦兹力提供向心力:qv1B=
解得:r1=
(2)带电粒子第二次被电场加速,由动能定理:qEd=
m
-
m
洛伦兹力提供向心力:qv2B=
解得:r2=
同理,通过A2时的半径:r3=
=
r1
所以:
=2r3-2r2=2(
-
)
(3)第n次通过Q时的半径:r2n-1=
r1
第n+1次通过Q时的半径:r2n+1=
r1
若An与An+1间的距离小于
,即:r2n+1-r2n-1=(
-
)r1<
r1
得:
-
<
当n≥5时,满足上面的条件.
答:(1)粒子第一次在Q右侧磁场区做圆运动的半径r1=
;
(2)粒子第一次和第二次通过Q平面的位置A1和A2之间的距离是2(
-
)
;
(3)设An与An+1间的距离小于
r1,则n值应≥5.
| 1 |
| 2 |
| v | 2 1 |
洛伦兹力提供向心力:qv1B=
m
| ||
| r1 |
解得:r1=
| m |
| qB |
|
(2)带电粒子第二次被电场加速,由动能定理:qEd=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
洛伦兹力提供向心力:qv2B=
m
| ||
| r2 |
解得:r2=
| m |
| qB |
|
同理,通过A2时的半径:r3=
| m |
| qB |
|
| 3 |
所以:
. |
| A1A2 |
| 3 |
| 2 |
| m |
| qB |
|
(3)第n次通过Q时的半径:r2n-1=
| 2n-1 |
第n+1次通过Q时的半径:r2n+1=
| 2n+1 |
若An与An+1间的距离小于
| r1 |
| 3 |
| 2n+1 |
| 2n-1 |
| 1 |
| 3 |
得:
| 2n+1 |
| 2n-1 |
| 1 |
| 3 |
当n≥5时,满足上面的条件.
答:(1)粒子第一次在Q右侧磁场区做圆运动的半径r1=
| m |
| qB |
|
(2)粒子第一次和第二次通过Q平面的位置A1和A2之间的距离是2(
| 3 |
| 2 |
| m |
| qB |
|
(3)设An与An+1间的距离小于
| 1 |
| 3 |
点评:本题关键是充分应用题给条件研究粒子第n次进入电场时的速度,穿出电场时速度.动能定理是常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?海淀区一模)如图所示是研究平行板电容器的电容大小与哪些因素有关的实验装置.将充好电的平行板电容器与电源断开并一板接地,另一板与外壳接地的静电计相连.当改变电容器两板之间的距离和两板正对面积时,实验发现静电计指针的张角随之改变.若电容器的电容用C表示,两板之间距离用d表示,两板正对面积用S表示,静电计指针张角用θ表示.则以下对该实验现象的判断正确的是( )
(2011?海淀区一模)如图所示是研究平行板电容器的电容大小与哪些因素有关的实验装置.将充好电的平行板电容器与电源断开并一板接地,另一板与外壳接地的静电计相连.当改变电容器两板之间的距离和两板正对面积时,实验发现静电计指针的张角随之改变.若电容器的电容用C表示,两板之间距离用d表示,两板正对面积用S表示,静电计指针张角用θ表示.则以下对该实验现象的判断正确的是( )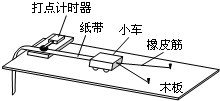 (2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是