题目内容
3. 如图所示,“凸”字形硬质金属线框质量为m,相邻各边相互垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l.匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面.开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef、pq边进入磁场前,线框做匀速运动.在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动.线框完全穿过磁场过程中产生的热量为Q.线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g.求:
如图所示,“凸”字形硬质金属线框质量为m,相邻各边相互垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l.匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面.开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef、pq边进入磁场前,线框做匀速运动.在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动.线框完全穿过磁场过程中产生的热量为Q.线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g.求:(1)线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的几倍;
(2)磁场上下边界间的距离H.
分析 (1)线框匀速进入(离开)磁场,重力与安培力平衡,根据平衡条件、安培力公式、切割公式、欧姆定律列式求解即可分别求出两个速度;
(2)由动能定理和功的计算公式,写出重力做的功W,然后结合功能关系即可求出磁场的宽度.
解答 解:(1)设线框dc边刚进入磁场时,线框的速度为v1,感应电动势 E=B•2lv1 ①
感应电流:I=$\frac{E}{R}$ ②
dc边受安培力的大小:F=BI•2l ③
由于做匀速运动,则:F=mg ④
由①~④式解得速度:${v}_{1}=\frac{mgR}{4{B}^{2}{l}^{2}}$⑤
设线框ab边将离开磁场时,线框的速度为v2,同理可得:
${v}_{2}=\frac{mgR}{{B}^{2}{l}^{2}}$ ⑥
所以:v2=4v1 ⑦
(2)在线框从开始下落到dc边刚进入磁场的过程中,重力做功WG=2mgl
根据动能定理得:2mgl=$\frac{1}{2}m{v}_{1}^{2}$ ⑧
线框完全穿过磁场的过程中,由功能关系得:
$mg(2l+H)=\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}+Q$ ⑨
联立⑦⑧⑨得:H=$\frac{Q}{mg}+28l$
答:(1)线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的4倍;
(2)磁场上下边界间的距离是$\frac{Q}{mg}+28l$.
点评 本题是电磁感应中的综合问题,全面考查电磁感应定律、欧姆定律以及动能定理、平衡条件等知识,分析清楚线框的运动过程、应用匀变速直线运动的速度位移公式、E=BLv、安培力公式、平衡条件、能量守恒定律、电流定义式即可正确解题.

练习册系列答案
相关题目
11.物理学重视逻辑,崇尚理性,其理论总是建立在对事实观察的基础上,下列说法正确的是( )
| A. | 天然放射现象说明原子核内部是有结构的 | |
| B. | 电子的发现使人们认识到原子具有核式结构 | |
| C. | α粒子散射实验的重要发现是电荷是量子化的 | |
| D. | 密立根油滴实验表明核外电子的轨道是不连续的 |
18. P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
 P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同.则( )| A. | P1的平均密度比P2的大 | B. | P1的“第一宇宙速度”比P2的小 | ||
| C. | s1的向心加速度比s2的大 | D. | s1的公转周期比s2的大 |
8. 如图所示为静电力演示仪,两金属极板分别固定于绝缘支架上,且正对平行放置,工作时两板分别接高压直流电源的正负极,表面镀铝的乒乓球用绝缘细线悬挂在两金属极板中间,则( )
如图所示为静电力演示仪,两金属极板分别固定于绝缘支架上,且正对平行放置,工作时两板分别接高压直流电源的正负极,表面镀铝的乒乓球用绝缘细线悬挂在两金属极板中间,则( )
 如图所示为静电力演示仪,两金属极板分别固定于绝缘支架上,且正对平行放置,工作时两板分别接高压直流电源的正负极,表面镀铝的乒乓球用绝缘细线悬挂在两金属极板中间,则( )
如图所示为静电力演示仪,两金属极板分别固定于绝缘支架上,且正对平行放置,工作时两板分别接高压直流电源的正负极,表面镀铝的乒乓球用绝缘细线悬挂在两金属极板中间,则( )| A. | 乒乓球的左侧感应出负电荷 | |
| B. | 乒乓球受到扰动后,会被吸在左极板上 | |
| C. | 乒乓球共受到电场力、重力和库仑力三个力的作用 | |
| D. | 用绝缘棒将乒乓球拔到与右极板接触,放开后乒乓球会在两极板间来回碰撞 |
15.以下说法正确的是( )
| A. | 所有原子核中的质子数和中子数都相等 | |
| B. | 在核反应中,质量数守恒、电荷数守恒 | |
| C. | 氢原子从高能级向低能级跃迁时能辐射出γ射线 | |
| D. | 只要光照射金属电极的时间足够长,就能发生光电效应 |
12. 如图所示,一倾斜放置的传送带静止不动,一质量为m的物块从传送带上端A沿传送带滑下,加速度为a1;若让传送带沿顺时针转动,让一质量为2m的物块也从传送带A沿传送带滑下,加速度为a2,两物块与传送带的动摩擦因数相同,则这两个加速度的大小关系为( )
如图所示,一倾斜放置的传送带静止不动,一质量为m的物块从传送带上端A沿传送带滑下,加速度为a1;若让传送带沿顺时针转动,让一质量为2m的物块也从传送带A沿传送带滑下,加速度为a2,两物块与传送带的动摩擦因数相同,则这两个加速度的大小关系为( )
 如图所示,一倾斜放置的传送带静止不动,一质量为m的物块从传送带上端A沿传送带滑下,加速度为a1;若让传送带沿顺时针转动,让一质量为2m的物块也从传送带A沿传送带滑下,加速度为a2,两物块与传送带的动摩擦因数相同,则这两个加速度的大小关系为( )
如图所示,一倾斜放置的传送带静止不动,一质量为m的物块从传送带上端A沿传送带滑下,加速度为a1;若让传送带沿顺时针转动,让一质量为2m的物块也从传送带A沿传送带滑下,加速度为a2,两物块与传送带的动摩擦因数相同,则这两个加速度的大小关系为( )| A. | a1<a2 | B. | a1>a2 | ||
| C. | a1=a2 | D. | a1、a2的大小关系不能确定 |
2.下列说法中正确的有 ( )
| A. | 光电效应实验中,只要入射光足够强,就能产生光电流 | |
| B. | 卢瑟福的α粒子散射实验结果表明电子是原子的组成部分,原子不可再分的观念被打破 | |
| C. | 天然放射现象中的γ射线是原子核受激发产生的 | |
| D. | 放射性元素的半衰期由其原子核内部结构 决定,与外界因素无关 | |
| E. | 氢原子从高能级向低能级跃迁时,放出光子,电势能减少 |
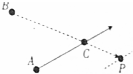 如图所示为两个足球运动员练习助攻进球的过程,其中BP在一条直线上,假设甲运动员在B处将足球以10m/s的速度沿直线BP的方向踢出,足球沿着地面向P处运动,足球运动的加速度大小为1m/s2,在A位置的乙运动员发现甲运动员将足球踢出去后,经过1s的反应时间后,开始匀加速向BP连线上的C处奔去,乙运动员的最大速度为8m/s,已知B、C两点间的距离为50m,A、C两点间的距离为56m.
如图所示为两个足球运动员练习助攻进球的过程,其中BP在一条直线上,假设甲运动员在B处将足球以10m/s的速度沿直线BP的方向踢出,足球沿着地面向P处运动,足球运动的加速度大小为1m/s2,在A位置的乙运动员发现甲运动员将足球踢出去后,经过1s的反应时间后,开始匀加速向BP连线上的C处奔去,乙运动员的最大速度为8m/s,已知B、C两点间的距离为50m,A、C两点间的距离为56m. 如图,一长为10cm的金属棒ab用两个完全相同的弹簧水平地悬挂在匀强磁场中,磁场的磁感应强度大小为0.1T,方向垂直于纸面向里,弹簧上端固定,下端与金属棒绝缘,金属棒通过开关与一电动势为12V的电池相连,电路总电阻为2Ω,已知开关断开时两弹簧的伸长量均为0.5cm,闭合开关,系统重新平衡后,两弹簧的伸长量与开关断开时相比均改变了0.3cm,重力加速度大小取10m/s2,判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量.
如图,一长为10cm的金属棒ab用两个完全相同的弹簧水平地悬挂在匀强磁场中,磁场的磁感应强度大小为0.1T,方向垂直于纸面向里,弹簧上端固定,下端与金属棒绝缘,金属棒通过开关与一电动势为12V的电池相连,电路总电阻为2Ω,已知开关断开时两弹簧的伸长量均为0.5cm,闭合开关,系统重新平衡后,两弹簧的伸长量与开关断开时相比均改变了0.3cm,重力加速度大小取10m/s2,判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量.