题目内容
13. 如图所示,一个初速度为零的电子通过电压为4500V的电场加速后,从C点沿水平方向飞入场强为1.5×105V/m的匀强电场中,到达该电场中另一点D时,电子的速度方向与场强方向的夹角正好是120°,求C、D两点沿场强方向的距离.
如图所示,一个初速度为零的电子通过电压为4500V的电场加速后,从C点沿水平方向飞入场强为1.5×105V/m的匀强电场中,到达该电场中另一点D时,电子的速度方向与场强方向的夹角正好是120°,求C、D两点沿场强方向的距离.
分析 由动能定理求出电子进入偏转电场时的速度,由运动学公式与牛顿第二定律求出距离.
解答 解:对电子加速过程,由动能定理:
$e{U}_{\;}=\frac{1}{2}m{{v}_{0}}^{2}$
得:${v}_{0}=\sqrt{\frac{2{U}_{\;}e}{m}}$
在偏转电场中,竖直方向:
vy=v0tan30°=at
根据牛顿第二定律得:$a=\frac{eE}{m}$
得:$t=\frac{1}{E}\sqrt{\frac{2mU}{3e}}$
CD两点沿场强方向的距离:
$y=\frac{1}{2}a{t}^{2}=\frac{U}{3E}=\frac{4500}{3×1.5×1{0}^{5}}=1{0}^{-2}m$
答:C、D两点沿场强方向的距离为10-2m.
点评 本题考查了电子在电场中的运动,分析清楚电子的运动过程,应用动能定理、运动学公式、牛顿第二定律即可正确解题,要掌握类平抛运动的运动规律.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
18.一个作匀加速直线运动的物体,其位移和时间的关系是x=20t-5t2,x与t的单位分别为m和s,则它的速度为零的时刻为( )
| A. | 2s | B. | 4s | C. | 8s | D. | 1s |
5.以下说法正确的是( )
| A. | 安培通过油滴实验发现了元电荷电量e | |
| B. | 奥斯特发现了电流的磁效应 | |
| C. | 洛伦兹潜心研究电流的热效应多年,并得到了电流产生热量的定量计算公式 | |
| D. | 法拉第首先提出了电场和磁场的概念,纠正了“超距作用”的错误观点 |
2.关于速度和加速度的关系,下列说法正确的是( )
| A. | 加速度很大,说明速度一定很大 | |
| B. | 加速度很大,说明速度的变化很快 | |
| C. | 加速度很大,说明速度的变化量很大 | |
| D. | 只要有加速度,速度就会不断增加 |
3.如图两个等量异种点电荷电场,AB为中垂线,且AO=BO,则( )
被过滤广告.
被过滤广告.
| A. | A、B两点场强相等 | B. | 正电荷从A运动到B,电势能增加 | ||
| C. | 正电荷从A运动到B,电势能减小 | D. | A、B两点电势差为零 |

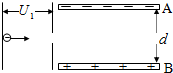 如图所示,电子由静止开始经电压为U1的加速电场后进入AB极板组成的平行板电容器,若电子从AB极板正中间射入,电子正好能穿出电场.已知:电子的电量为e,质量为m,AB两极板间的电压为U2,距离为d,重力不计,求:
如图所示,电子由静止开始经电压为U1的加速电场后进入AB极板组成的平行板电容器,若电子从AB极板正中间射入,电子正好能穿出电场.已知:电子的电量为e,质量为m,AB两极板间的电压为U2,距离为d,重力不计,求: