题目内容
 如图所示,质量M=5.0kg的平板车A原来静止于光滑水平面上,A与竖直固定挡板的距离d=0.050m.质量m=3.0kg的滑块B以大小v0=1.64m/s的初速水平向右滑上平板车.一段时间后,A车与挡板发生碰撞.设车碰挡板前后的速度大小不变但方向相反,且碰撞的时间极短.已知A、B之间的动摩擦因数μ=0.15,A的车板足够长,重力加速度g=10m/s2.求:
如图所示,质量M=5.0kg的平板车A原来静止于光滑水平面上,A与竖直固定挡板的距离d=0.050m.质量m=3.0kg的滑块B以大小v0=1.64m/s的初速水平向右滑上平板车.一段时间后,A车与挡板发生碰撞.设车碰挡板前后的速度大小不变但方向相反,且碰撞的时间极短.已知A、B之间的动摩擦因数μ=0.15,A的车板足够长,重力加速度g=10m/s2.求:(1)A车第一次碰到挡板前瞬间,车A和滑块B的速度vA和vB各是多大?
(2)当A车与挡板所有可能的碰撞都发生后,车A和滑块B稳定后的速度是多少?
分析:(1)根据动能定理求出A车第一次碰到挡板时的速度大小,从而得出与挡板碰后的速度大小,抓住车A和滑块动量守恒,求出车与挡板碰撞前瞬间滑块的速度大小.
(2)假设车到第二次碰到挡板之前,B已经停在车上,则车从第一次碰到挡板之后到第二次碰到挡板之前的这段时间内,车A和滑块B组成的系统动量守恒,根据动量守恒求出共同的速度,因为小车与挡板碰撞时间极短,碰撞的过程中,A的速度大小不变,方向反向,B的速度不变,再根据动量守恒定律求出车A和滑块B稳定后的速度.
(2)假设车到第二次碰到挡板之前,B已经停在车上,则车从第一次碰到挡板之后到第二次碰到挡板之前的这段时间内,车A和滑块B组成的系统动量守恒,根据动量守恒求出共同的速度,因为小车与挡板碰撞时间极短,碰撞的过程中,A的速度大小不变,方向反向,B的速度不变,再根据动量守恒定律求出车A和滑块B稳定后的速度.
解答:解:(1)假设A车第一次碰到挡板前一直做加速运动
对车A,由动能定理有
fd=μmgd=
MvA2 ①
代入数据解得vA=0.30m/s ②
车碰到挡板前,车A和滑块B组成的系统动量守恒,有
mv0=mvB+MvA ③
将vA=0.30m/s和其它数据代入解得
vB=1.14m/s ④
此时vB>vA,说明此前B一直与车A发生相对滑动,车A一直加速.
因此车碰到挡板前,车A和滑块B的速度分别是
vA=0.30m/s,vB=1.14m/s
(2)假设车到第二次碰到挡板之前,B已经停在车上,则车从第一次碰到挡板之后到第二次碰到挡板之前的这段时间内,车A和滑块B组成的系统动量守恒,取向右方向为正方向,有
mvB-MvA=(m+M)v′⑤
代入数据解得v′=0.24m/s(方向向右) ⑥
因为v′<vA,说明车从第一次碰到挡板之后到第二次碰到挡板之前的这段时间内,车A先向左做减速运动,再向右做加速运动,最后保持匀速运动直到第二次碰撞挡板.
车到第二次碰到挡板之后,系统的总动量方向向左,由动量守恒定律可得
mv′-Mv′=(m+M)v″⑦
代入数据解得v″=-0.03m/s(负号方向向左) ⑧
答:(1)A车第一次碰到挡板前瞬间,车A和滑块B的速度vA和vB各是0.30m/s、1.14m/s.
(2)当A车与挡板所有可能的碰撞都发生后,车A和滑块B稳定后的速度是0.03m/s,反向向左.
对车A,由动能定理有
fd=μmgd=
| 1 |
| 2 |
代入数据解得vA=0.30m/s ②
车碰到挡板前,车A和滑块B组成的系统动量守恒,有
mv0=mvB+MvA ③
将vA=0.30m/s和其它数据代入解得
vB=1.14m/s ④
此时vB>vA,说明此前B一直与车A发生相对滑动,车A一直加速.
因此车碰到挡板前,车A和滑块B的速度分别是
vA=0.30m/s,vB=1.14m/s
(2)假设车到第二次碰到挡板之前,B已经停在车上,则车从第一次碰到挡板之后到第二次碰到挡板之前的这段时间内,车A和滑块B组成的系统动量守恒,取向右方向为正方向,有
mvB-MvA=(m+M)v′⑤
代入数据解得v′=0.24m/s(方向向右) ⑥
因为v′<vA,说明车从第一次碰到挡板之后到第二次碰到挡板之前的这段时间内,车A先向左做减速运动,再向右做加速运动,最后保持匀速运动直到第二次碰撞挡板.
车到第二次碰到挡板之后,系统的总动量方向向左,由动量守恒定律可得
mv′-Mv′=(m+M)v″⑦
代入数据解得v″=-0.03m/s(负号方向向左) ⑧
答:(1)A车第一次碰到挡板前瞬间,车A和滑块B的速度vA和vB各是0.30m/s、1.14m/s.
(2)当A车与挡板所有可能的碰撞都发生后,车A和滑块B稳定后的速度是0.03m/s,反向向左.
点评:解决本题的关键理清A、B的运动过程,抓住AB系统动量守恒,结合动量守恒定律和动能定理进行求解.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
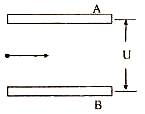
 如图所示,质量m=5×10-8kg的带电粒子,以初速v0=2m/s的速度从水平放置的平行金属板A、B的中央,水平飞入电场,已知金属板长0.1m,板间距离d=2×10-2m,当UAB=1000V时,带电粒子恰好沿直线穿过电场,若两极板间的电势差可调,要使粒子能从两板间飞出,UAB的变化范围是多少?(g取10m/s2)
如图所示,质量m=5×10-8kg的带电粒子,以初速v0=2m/s的速度从水平放置的平行金属板A、B的中央,水平飞入电场,已知金属板长0.1m,板间距离d=2×10-2m,当UAB=1000V时,带电粒子恰好沿直线穿过电场,若两极板间的电势差可调,要使粒子能从两板间飞出,UAB的变化范围是多少?(g取10m/s2)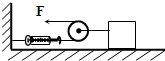 如图所示,质量m=5㎏的物体在力F的作用下,以5m/s的速度沿水平面作匀速直线运动(滑轮重及与绳间摩擦不计),此时弹簧秤的读数为2N,物体和水平面间的摩擦力是
如图所示,质量m=5㎏的物体在力F的作用下,以5m/s的速度沿水平面作匀速直线运动(滑轮重及与绳间摩擦不计),此时弹簧秤的读数为2N,物体和水平面间的摩擦力是