题目内容
15.小船在200m宽的河中横渡,水流速度是2m/s,船在静水中速度是4m/s,求(1)小船怎样才能沿最短路径度过河去?需时多少?
(2)小船怎样才能以最短时间度过河去?需时多少?
分析 (1)当合速度与河岸垂直时,将运行到正对岸,求出合速度的大小,根据河岸求出渡河的时间.
(2)将小船运动分解为沿河岸方向和垂直于河岸方向,根据垂直于河岸方向上的速度求出渡河的时间,再根据沿河岸方向上的运动求出沿河岸方向上的位移.
解答 解:(1)小船沿最短路径渡河即合速度垂直河岸v合=$\sqrt{{v}_{c}^{2}-{v}_{s}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(m/s)
即偏向上游夹角为θ,则有:cosθ=$\frac{2}{4}$,
解得:θ=60°
渡河时间为:t=$\frac{d}{{v}_{合}}$=$\frac{200}{2\sqrt{3}}$=$\frac{100\sqrt{3}}{3}$(s)
(2)小船渡河最短时间即船身与河岸垂直:t=$\frac{d}{{v}_{c}}$=$\frac{200}{4}$=50(s)
答:(1)小船偏向上游与河岸夹角为60°时,渡河路最短径,需时$\frac{100\sqrt{3}}{3}$s;
(2)小船在静水中的速度垂直河岸时,渡河时间最短,即为50s.
点评 解决本题的关键知道分运动与合运动具有等时性,以及各分运动具有独立性,互不干扰.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5.关于摩擦力与弹力的关系,下列说法中正确的是( )
| A. | 有弹力一定有摩擦力 | |
| B. | 有弹力不一定有摩擦力? | |
| C. | 有摩擦力一定有弹力? | |
| D. | 同一接触面上的弹力和摩擦力的方向一定平行 |
4.美国国家航空航天局(简称NASA)发布声明,证实通过开普勒太空望远镜发现了“第二地球”、一颗名为“开普勒22b”的行星,该行星的半径约是地球的2.4倍,“开普勒22b”绕恒星“开普勒22”运动的周期为290天,轨道半径为R1;地球绕太阳运动的轨道半径为R2,测得R1:R2=0.85.由上述信息可判断下列说法正确的是( )
| A. | 若“开普勒22b”与地球密度相同,则它与地球表面的重力加速度之比约为1:2.4 | |
| B. | 若“开普勒22b”与地球密度相同,则它与地球表面的重力加速度之比约为2.4:1 | |
| C. | 恒星“开普勒22”与太阳的质量之比约为1:10 | |
| D. | 恒星“开普勒22”与太阳的质量之比约为1:1 |
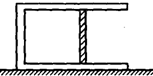 如图所示,一水平放置的固定不动的圆柱形汽缸,质量M=2kg,活塞质量m=1kg,封闭了一定质量的理想气体,初温为27℃,气柱长度L=100cm,截面积S=10cm2.开始时,内、外气压均为105Pa,活塞与汽缸的最大静摩擦力为5N,问:使气体温度缓慢升高到37℃和127℃时,活塞相对地面的位移分别是多少?
如图所示,一水平放置的固定不动的圆柱形汽缸,质量M=2kg,活塞质量m=1kg,封闭了一定质量的理想气体,初温为27℃,气柱长度L=100cm,截面积S=10cm2.开始时,内、外气压均为105Pa,活塞与汽缸的最大静摩擦力为5N,问:使气体温度缓慢升高到37℃和127℃时,活塞相对地面的位移分别是多少?