题目内容
 如图所示,在直角三角形区域ABC内存在着平行于AC方向的匀强电场,AC边长为L,一质量为m,电荷量+q的带电粒子以初速度v0从A点沿AB方向进入电场,垂直通过BC边的中点,则粒子从BC出来时的水平分速度vx=
如图所示,在直角三角形区域ABC内存在着平行于AC方向的匀强电场,AC边长为L,一质量为m,电荷量+q的带电粒子以初速度v0从A点沿AB方向进入电场,垂直通过BC边的中点,则粒子从BC出来时的水平分速度vx=V0
V0
,电场强度的大小E=2m
| ||
| qL |
2m
| ||
| qL |
分析:带电粒子垂直进入电场做类平抛运动,水平方向做匀速直线运动,速度不变.粒子垂直通过BC边的中点,速度方向与水平方向的夹角等于∠C,竖直位移等于
,水平位移等于
tan∠C.根据牛顿第二定律和运动学公式分别两个分位移的关系和两个分速度的关系,求出E的大小.
| L |
| 2 |
| L |
| 2 |
解答:解:带电粒子垂直进入电场做类平抛运动,水平方向做匀速直线运动,粒子从BC出来时的水平分速度vx=V0.
设粒子垂直通过BC边中点时水平位移为x,竖直位移为y,∠C=θ
由题x=
tanθ=v0t ①
y=
=
at2=
t2 ②
由①②联立得
=
(
)2③
设粒子经过BC中点时竖直方向分速度这vy,
则vy=v0tanθ
又vy2=2ay 得到v02tan2θ=2
=
④
tan2θ=
⑤
将⑤代入③解得
E=
故本题答案是:V0;
设粒子垂直通过BC边中点时水平位移为x,竖直位移为y,∠C=θ
由题x=
| L |
| 2 |
y=
| L |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
由①②联立得
| L |
| 2 |
| 1 |
| 2 |
| qE |
| m |
| Ltanθ |
| 2v0 |
设粒子经过BC中点时竖直方向分速度这vy,
则vy=v0tanθ
又vy2=2ay 得到v02tan2θ=2
| qE |
| m |
| L |
| 2 |
| qEL |
| m |
tan2θ=
| qEL | ||
|
将⑤代入③解得
E=
2m
| ||
| qL |
故本题答案是:V0;
2m
| ||
| qL |
点评:本题粒子做类平抛运动,既要分解位移,又要分解速度,考查综合分析和应用的能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 (2013?开封模拟)如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动到达P点的时间相同.下列说法正确的是( )
(2013?开封模拟)如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动到达P点的时间相同.下列说法正确的是( ) 如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现将OD边水平放置,让小物块无初速从C滑到D;然后将OC边水平放置,再让小物块无初速从D滑到C.已知小物块两次滑动到达P点的时间相同.下列说法正确的是( )
如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现将OD边水平放置,让小物块无初速从C滑到D;然后将OC边水平放置,再让小物块无初速从D滑到C.已知小物块两次滑动到达P点的时间相同.下列说法正确的是( )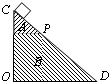 如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块无初速从C滑到D;然后将OC边水平放置,再让小物块无初速从D滑到C,小物块两次滑动到达P点的时间相同.下列说法正确的是( )
如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块无初速从C滑到D;然后将OC边水平放置,再让小物块无初速从D滑到C,小物块两次滑动到达P点的时间相同.下列说法正确的是( ) (2011?上海模拟)如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动经过P点的时间相同.下列说法正确的是( )
(2011?上海模拟)如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动经过P点的时间相同.下列说法正确的是( )