��Ŀ����
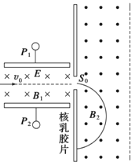
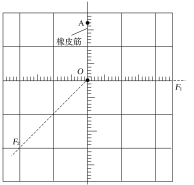
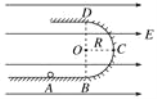
����Ŀ����ͼ��ʾ��ABCDΪ�������ڳ�ǿΪE��104V/m��ˮƽ��ǿ�糡�еľ�Ե�⻬��������й����BCD�����ǰ뾶ΪR�İ�Բ���������ˮƽ�������Բ�����У�AΪˮƽ����ϵ�һ�㣬����AB��R��0.2m����һ����m��0.1kg��������q��10��4C��С����ˮƽ�����A���ɾ�ֹ��ʼ�ͷź��ڹ�����ڲ��˶���(gȡ10 m/s2)��
(1)������C��ʱ���ٶ��Ƕ��
(2)����С��ȫͨ��D�㣬��ʼ�ͷŵ���B�����ٶ�Զ��
���𰸡�(1)2 m/s��(2)0.5 m
��������
(1)��A�㵽C��Ӧ�ö��ܶ�����
Eq(AB��R)��mgR��![]()
���
vC��2m/s
(2)��D�㣬С��Ҫ��ȫͨ������
mg��m![]()
���ͷŵ��B��ľ���Ϊx���ɶ��ܶ����ã�
Eqx��mg2R��![]()
������ʽ�����ɵ�
x��0.5m.

 ÿ��10���ӿ�����������������ϵ�д�
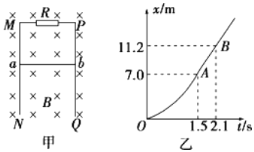
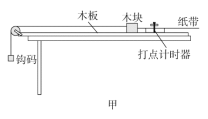
ÿ��10���ӿ�����������������ϵ�д�����Ŀ��������ͼ1��ʾ��ʵ��װ��̽���������������嶯�ܱ仯�Ĺ�ϵ��С��������ΪM=200.0g�����������Ϊm=10.0g������ʱ���ĵ�ԴΪ50Hz�Ľ����磮

��1���ҹ���ǰ��Ϊ������Ħ������Ӱ�죬Ӧ����ľ���Ҳ�ĸ߶ȣ�ֱ����������С���۲쵽_____��
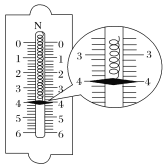
��2�����Ϲ��룬��ʵ��Ҫ������һ��ֽ����ͼ2��ʾ��ѡ��ijһ��ΪO��һ��ÿ��4����ʱ��ȡһ�������㣮�ÿ̶ȳ��������ڼ������ľ�����x����¼��ֽ���ϣ���������������ʱС�����ٶ�v�����д����������1��ʱС�����ٶ�v1=_____m/s��
��3���������������λС���ܵ���������ȡg=9.80m/s2������W=mg��x���������С�����Ĺ�W������Ek=![]() Mv2���С�����ܣ���������ܵı仯����Ek�����������±���
Mv2���С�����ܣ���������ܵı仯����Ek�����������±���
W/��10��3J | 2.45 | 2.92 | 3.35 | 3.81 | 4.26 |
��Ek/��10��3J | 2.31 | 2.73 | 3.12 | 3.61 | 4.00 |
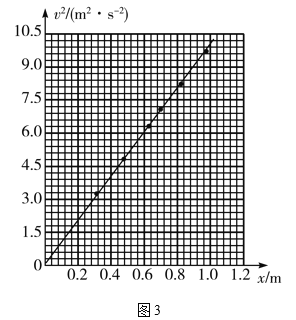
����ݱ��е����ݣ��ڴ���ķ���ֽ��������Ek��Wͼ��
��4��ʵ������������Ek������С��W��ijͬѧ����������С����������С�ڹ���������ɵģ�������С���������������ݿ����С���ܵ���ʵ������F=_____��