Question

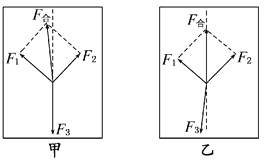
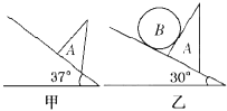
【题目】截面为直角三角形的木块A质量为M，放在倾角为θ的斜面上，当θ=37°时，木块恰能静止在斜面上。现将θ改为30°，在A与斜面间放一质量为m的光滑圆柱体B，如图乙，（sin37°=0．6，cos37°=0．8）则 （ ）

A．A、B仍一定静止于斜面上

B．A、B可能静止于斜面上

C．若M=2m，则A受到的摩擦力为mg

D．若M=8m，则A受到斜面的摩擦力为mg

Answer 1

【答案】BD

【解析】

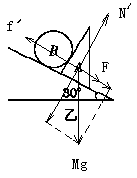
试题分析：由题意可知，当θ=37°时，木块恰能静止在斜面上，则有：μMgcos37°=Mgsin37°；代入数据解得：μ=0．75．现将θ改为30°，在A与斜面间放一质量为m的光滑圆柱体B，对A受力分析，则有：f′=μN′

N′=Mgcos30°；而F=mgsin30°；当f′＜mgsin30°+Mgsin30°，则A相对斜面向下滑动，当f′＞mgsin30°+Mgsin30°，则A相对斜面不滑动，因此A、B是否静止在斜面上，由B对A弹力决定，故A错误，B正确；

若M=2m，则mgsin30°+Mgsin30°=Mg；而f′=μN′=0．75×Mgcos30°=Mg；因f′＜mgsin30°+Mgsin30°，A滑动，A受到斜面的滑动摩擦力，大小为f′=μN′=0．75×Mgcos30°=Mg=mg，故C错误；若M=8m，则mgsin30°+Mgsin30°=Mg；而f′=μN′=0．75×Mgcos30°=Mg；因f′＞mgsin30°+Mgsin30°，A不滑动，A受到斜面的静摩擦力，大小为：mgsin30°+Mgsin30°=Mg=mg，故D正确；故选BD．