题目内容
 如图所示,质是为M的小车置于光滑的水平面上,小车的上表面粗糙且足够长,质量为m的小木块以初速度v滑上车的上表面,最终共同向右运动,则下列说法中正确的是( )
如图所示,质是为M的小车置于光滑的水平面上,小车的上表面粗糙且足够长,质量为m的小木块以初速度v滑上车的上表面,最终共同向右运动,则下列说法中正确的是( )分析:以小车和木块组成的系统为研究对象所受合外力为零,因此系统动量守恒,根据动量守恒列方程即可解答.
相对运动过程中系统机械能减小,转化为摩擦产生的内能.
相对运动过程中系统机械能减小,转化为摩擦产生的内能.
解答:解:A、以小车和木块组成的系统为研究对象所受合外力为零,因此系统动量守恒,
由于摩擦力的作用,m速度减小,M速度增大,m速度减小到最小时,M速度达最大,最后m、M以共同速度运动.
mv=(m+M)v′
v′=
相对运动过程中系统机械能减小,转化为摩擦产生的内能,根据能量守恒得:
E损=
mv2-
(m+M)v′2
故A、D正确.
B、车表面粗糙,小车与木块间的力属于内力,不是判断系统动量是否守恒的条件.故B错误.
C、根据A选项分析,小车M获得动量Mv′与车面粗糙程度无关,故C错误.
故选AD.
由于摩擦力的作用,m速度减小,M速度增大,m速度减小到最小时,M速度达最大,最后m、M以共同速度运动.
mv=(m+M)v′
v′=
| mv |
| (M+m) |
相对运动过程中系统机械能减小,转化为摩擦产生的内能,根据能量守恒得:
E损=
| 1 |
| 2 |
| 1 |
| 2 |
故A、D正确.
B、车表面粗糙,小车与木块间的力属于内力,不是判断系统动量是否守恒的条件.故B错误.
C、根据A选项分析,小车M获得动量Mv′与车面粗糙程度无关,故C错误.
故选AD.
点评:应用动量守恒定律时要清楚研究的对象和守恒条件.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.

练习册系列答案
相关题目
 如图所示,质量均为m的A、B两个小球,用长为2L的轻质杆相连接,在竖直平面内绕固定轴O沿顺时针方向自由转动(转轴在杆的中点),不计一切摩擦,某时刻A、B球恰好在如图所示的位置,A、B球的线速度大小均为v,下列说法正确的是( )
如图所示,质量均为m的A、B两个小球,用长为2L的轻质杆相连接,在竖直平面内绕固定轴O沿顺时针方向自由转动(转轴在杆的中点),不计一切摩擦,某时刻A、B球恰好在如图所示的位置,A、B球的线速度大小均为v,下列说法正确的是( )| A、运动过程中B球机械能守恒 | B、运动过程中B球速度大小不变 | C、B球在最低点到最高点的过程中,克服重力做功的功率先增大后减小 | D、B球在最低点到最高点的过程中,克服重力做功的功率不变 |
 如图所示,质量均为m的两物体b、c分别与轻质弹簧两端相连接,将它们静止放在地在地面上.弹簧劲度系数为k.一质量也为m 小物体a从距b物体h高处由静止开始下落.a与b相碰后立即粘在一起向下运动,以后不再分开.已知重力加速度为g,不计空气阻力,弹簧始终处于弹性限度内.在a与b一起向下运动的过程中,下列判断正确的是( )
如图所示,质量均为m的两物体b、c分别与轻质弹簧两端相连接,将它们静止放在地在地面上.弹簧劲度系数为k.一质量也为m 小物体a从距b物体h高处由静止开始下落.a与b相碰后立即粘在一起向下运动,以后不再分开.已知重力加速度为g,不计空气阻力,弹簧始终处于弹性限度内.在a与b一起向下运动的过程中,下列判断正确的是( )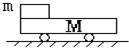

 ,并且可以计算出损失的能量
,并且可以计算出损失的能量