题目内容
16.下列公式书写正确的是( )| A. | 向心力F向=mv2r | B. | 万有引力F引=G$\frac{Mm}{r}$ | C. | 动能Ek=$\frac{1}{2}$m2v2 | D. | 重力势能EP=mgh |
分析 确定各项的正确表达式,遂项判断即可.
解答 解:A、向心力F=$;m\frac{{v}^{2}}{r}$$m\frac{{v}^{2}}{r}$,则A错误
B、万有引力F=$G\frac{Mm}{{r}^{2}}$,则B错误
C、动能${E}_{K}=\frac{1}{2}m{v}^{2}$,则C错误
D、重力势能EP=mgh,则D正确
故选:D
点评 要求能熟练掌握各常用表达式,不难.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
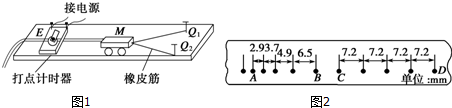
7.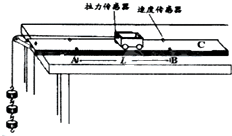 某实验小组利用拉力传感器和速度传感器探究“动能定理”,如图,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平桌面上相距50.0cm的A、B两点各安装一个速度传感器记录小车通过A、B时的速度大小.小车中可以放置砝码.
某实验小组利用拉力传感器和速度传感器探究“动能定理”,如图,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平桌面上相距50.0cm的A、B两点各安装一个速度传感器记录小车通过A、B时的速度大小.小车中可以放置砝码.
(1)实验主要步骤如下:
①测量小车和砝码以及拉力传感器的总质量和拉力传感器的总质量M1;把细线的一端固定在拉力传感器上另一端通过定滑轮与钩码相连;正确连接所需电路;
②将小车停在C点,小车和砝码以及拉力传感器的总质量,小车在细线拉动下运动,记录细线拉力及小车通过A、B时的速度.
③在小车中增加砝码,或小车和砝码,重复②的操作.
(2)表1是他们测得的一组数据,其中M是M1与小车中砝码质量之和,|v22-v21|是两个速度传感器记录速度的平方差,可以据此计算出动能变化量△E,F是拉力传感器受到的拉力,W是F在A、B间所作的功.表格中△E3=0.600J,W3=0.610J.(结果保留三位有效数字)
表1 数据记录表
 某实验小组利用拉力传感器和速度传感器探究“动能定理”,如图,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平桌面上相距50.0cm的A、B两点各安装一个速度传感器记录小车通过A、B时的速度大小.小车中可以放置砝码.
某实验小组利用拉力传感器和速度传感器探究“动能定理”,如图,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平桌面上相距50.0cm的A、B两点各安装一个速度传感器记录小车通过A、B时的速度大小.小车中可以放置砝码.(1)实验主要步骤如下:
①测量小车和砝码以及拉力传感器的总质量和拉力传感器的总质量M1;把细线的一端固定在拉力传感器上另一端通过定滑轮与钩码相连;正确连接所需电路;
②将小车停在C点,小车和砝码以及拉力传感器的总质量,小车在细线拉动下运动,记录细线拉力及小车通过A、B时的速度.
③在小车中增加砝码,或小车和砝码,重复②的操作.
(2)表1是他们测得的一组数据,其中M是M1与小车中砝码质量之和,|v22-v21|是两个速度传感器记录速度的平方差,可以据此计算出动能变化量△E,F是拉力传感器受到的拉力,W是F在A、B间所作的功.表格中△E3=0.600J,W3=0.610J.(结果保留三位有效数字)
表1 数据记录表
| 次数 | M/kg | |v22-v21|/(m/s)2 | △E/J | F/N | W/J |
| 1 | 0.500 | 0.760 | 0.190 | 0.400 | 0.200 |
| 2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
| 3 | 0.500 | 2.40 | △E3 | 1.220 | W3 |
| 4 | 1.000 | 2.40 | 1.20 | 2.420 | 1.21 |
| 5 | 1.000 | 2.84 | 1.42 | 2.860 | 1.43 |
4.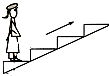 为了节省能量,香坊万达商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则在加速过程中,下列说法中正确的是( )
为了节省能量,香坊万达商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则在加速过程中,下列说法中正确的是( )
 为了节省能量,香坊万达商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则在加速过程中,下列说法中正确的是( )
为了节省能量,香坊万达商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则在加速过程中,下列说法中正确的是( )| A. | 顾客受到三个力的作用 | B. | 顾客受到摩擦力的方向沿斜面向上 | ||
| C. | 扶梯对顾客没有摩擦力的作用 | D. | 顾客对扶梯的压力等于顾客的重量 |
1. 如图所示,两物体与水平面间的摩擦因数不同,质量也不同,它们所受的拉力F1和推力F2及力与水平方向的夹角相等,两物体在F1和 F2的作用下发生的位移相同,则 F1和F2对物体所做的功W1和W2的关系是( )
如图所示,两物体与水平面间的摩擦因数不同,质量也不同,它们所受的拉力F1和推力F2及力与水平方向的夹角相等,两物体在F1和 F2的作用下发生的位移相同,则 F1和F2对物体所做的功W1和W2的关系是( )
 如图所示,两物体与水平面间的摩擦因数不同,质量也不同,它们所受的拉力F1和推力F2及力与水平方向的夹角相等,两物体在F1和 F2的作用下发生的位移相同,则 F1和F2对物体所做的功W1和W2的关系是( )
如图所示,两物体与水平面间的摩擦因数不同,质量也不同,它们所受的拉力F1和推力F2及力与水平方向的夹角相等,两物体在F1和 F2的作用下发生的位移相同,则 F1和F2对物体所做的功W1和W2的关系是( )| A. | W1=W2 | B. | W1>W2 | C. | W1<W2 | D. | 无法确定 |
5.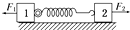 质量均为5kg的物块1、2放在光滑水平面上并用轻质弹簧秤相连,如图所示,今对物块1、2分别施以方向相反的水平力F1、F2且F1=20N、F2=10N,则弹簧秤的示数为( )
质量均为5kg的物块1、2放在光滑水平面上并用轻质弹簧秤相连,如图所示,今对物块1、2分别施以方向相反的水平力F1、F2且F1=20N、F2=10N,则弹簧秤的示数为( )
 质量均为5kg的物块1、2放在光滑水平面上并用轻质弹簧秤相连,如图所示,今对物块1、2分别施以方向相反的水平力F1、F2且F1=20N、F2=10N,则弹簧秤的示数为( )
质量均为5kg的物块1、2放在光滑水平面上并用轻质弹簧秤相连,如图所示,今对物块1、2分别施以方向相反的水平力F1、F2且F1=20N、F2=10N,则弹簧秤的示数为( )| A. | 30 N | B. | 15 N | C. | 20 N | D. | 10 N |
6.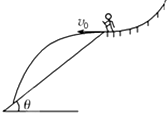 第22届冬季奥林匹克运动会于2014年2月7日至2月23日在俄罗斯索契市举行.跳台滑雪是比赛项目之一,利用自然山形建成的跳台进行,某运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,如图所示,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )
第22届冬季奥林匹克运动会于2014年2月7日至2月23日在俄罗斯索契市举行.跳台滑雪是比赛项目之一,利用自然山形建成的跳台进行,某运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,如图所示,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )
 第22届冬季奥林匹克运动会于2014年2月7日至2月23日在俄罗斯索契市举行.跳台滑雪是比赛项目之一,利用自然山形建成的跳台进行,某运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,如图所示,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )
第22届冬季奥林匹克运动会于2014年2月7日至2月23日在俄罗斯索契市举行.跳台滑雪是比赛项目之一,利用自然山形建成的跳台进行,某运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,如图所示,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )| A. | 如果v0不同,该运动员落到雪坡时的位置不同,速度方向也不同 | |
| B. | 如果v0不同,该运动员落到雪坡时的位置相同,但速度方向不同 | |
| C. | 运动员落到雪坡时的速度大小是$\frac{v_0}{cosθ}$ | |
| D. | 运动员在空中经历的时间是$\frac{{2{v_0}tanθ}}{g}$ |
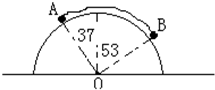 如图所示,AB两球用轻绳相连静止在光滑半圆柱面上,若A的质量为m,则B的质量为多少?(sin37°=0.6 cos37°=0.8)
如图所示,AB两球用轻绳相连静止在光滑半圆柱面上,若A的质量为m,则B的质量为多少?(sin37°=0.6 cos37°=0.8)