题目内容
 如图所示,处于匀强磁场中的两根足够长、电阻不计的光滑平行金属导轨相距L=1m,导轨平面与水平面成θ=30°角,下端连接阻值为R=0.8Ω的电阻,匀强磁场方向与导轨平面垂直,磁感强度大小B=1T;质量为m=0.1kg、电阻r=0.2Ω金属棒放在两导轨上,棒与导轨垂直并保持良好接触.g取10m/s2.求:
如图所示,处于匀强磁场中的两根足够长、电阻不计的光滑平行金属导轨相距L=1m,导轨平面与水平面成θ=30°角,下端连接阻值为R=0.8Ω的电阻,匀强磁场方向与导轨平面垂直,磁感强度大小B=1T;质量为m=0.1kg、电阻r=0.2Ω金属棒放在两导轨上,棒与导轨垂直并保持良好接触.g取10m/s2.求:(1)金属棒沿导轨由静止开始下滑时的加速度大小;
(2)金属棒ab所能获得的最大速度;
(3)若属棒ab沿斜面下滑0.2m时恰好获得最大速度,求在此过程中回路一共生热多少焦?
分析:(1)金属棒开始下滑的初速度为零,回路中没有感应电流,根据牛顿第二定律求解加速度大小;
(2)当导体棒匀速运动时,速度最大,由平衡条件和安培力公式,即可求得ab所能获得的最大速度;
(3)根据全过程中能转化和守恒规律,列方程求解焦耳热.
(2)当导体棒匀速运动时,速度最大,由平衡条件和安培力公式,即可求得ab所能获得的最大速度;
(3)根据全过程中能转化和守恒规律,列方程求解焦耳热.
解答:解:(1)金属棒开始下滑的初速度为零,根据牛顿第二定律得:
mgsinθ=ma
代人数据解得:a=5m/s2
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡有:
mgsinθ=FA
FA=BIL=B
L=
mgsinθ=
最大速度为:vm=
=0.5m/s
(3)根据全过程中能的转化和守恒规律,有:mgxsinθ=
mv2+Q
所以全过程中系统产生的热为:Q=mgxsinθ-
mv2=0.0875J
答:(1)金属棒沿导轨由静止开始下滑时的加速度大小为5m/s2.
(2)金属棒ab所能获得的最大速度为0.5m/s;
(3)若属棒ab沿斜面下滑0.2m时恰好获得最大速度,在此过程中回路一共生热0.0875J.
mgsinθ=ma
代人数据解得:a=5m/s2
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡有:
mgsinθ=FA
FA=BIL=B
| Blv |
| R+r |
| B2L2v |
| R+r |
mgsinθ=
| B2L2vm |
| (R+r) |
最大速度为:vm=
| mgsinθ(R+r) |
| B2L2 |
(3)根据全过程中能的转化和守恒规律,有:mgxsinθ=
| 1 |
| 2 |
所以全过程中系统产生的热为:Q=mgxsinθ-
| 1 |
| 2 |
答:(1)金属棒沿导轨由静止开始下滑时的加速度大小为5m/s2.
(2)金属棒ab所能获得的最大速度为0.5m/s;
(3)若属棒ab沿斜面下滑0.2m时恰好获得最大速度,在此过程中回路一共生热0.0875J.
点评:电磁感应中导体切割引起的感应电动势在考试中涉及较多,关键要正确分析导体棒受力情况,运用平衡条件、牛顿第二定律和功能关系进行求解.

练习册系列答案
相关题目
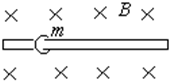 如图所示,质量为m、带电量为+q的滑环,套在水平放置的足够长的固定绝缘横杆上,横杆表面粗糙,整个装置处于磁感强度为B的匀强磁场中,现给滑环一个水平向右的速度v,使其向右运动.(环的直径大于杆的直径,环很小可以当成质点研究)
如图所示,质量为m、带电量为+q的滑环,套在水平放置的足够长的固定绝缘横杆上,横杆表面粗糙,整个装置处于磁感强度为B的匀强磁场中,现给滑环一个水平向右的速度v,使其向右运动.(环的直径大于杆的直径,环很小可以当成质点研究) (2012?上海模拟)如图所示,倾角为α的斜面上放有一通电的矩形线圈,电流方向沿adcba,线圈的ad边和bc边处于水平方向,若整个装置放在一个磁感强度方向竖直向上的匀强磁场之中,线圈处于平衡状态,那么下列说法中正确的有( )
(2012?上海模拟)如图所示,倾角为α的斜面上放有一通电的矩形线圈,电流方向沿adcba,线圈的ad边和bc边处于水平方向,若整个装置放在一个磁感强度方向竖直向上的匀强磁场之中,线圈处于平衡状态,那么下列说法中正确的有( )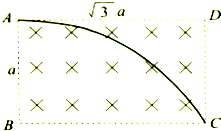 如图所示,一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场,速度方向与磁感线垂直.且平行于矩形空间的其中一边,矩形空间边长为
如图所示,一束电子流以速率v通过一个处于矩形空间的大小为B的匀强磁场,速度方向与磁感线垂直.且平行于矩形空间的其中一边,矩形空间边长为