题目内容
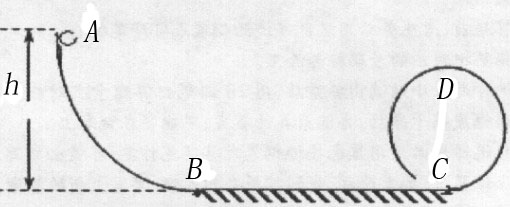
如下图所示,半径R="0.40" m 的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m="0.10" kg的小球,以初速度v0="7.0" m/s在水平地面上向左做加速度a="3.0" m/s2的匀减速直线运动,运动4.0 m后,冲上竖直半圆环,最后小球落在C点.求A、C间的距离.(取重力加速度g="10" m/s2)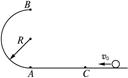

sAC="1.2" m
设小球到达A点的速率为vA,到达B点的速率为vB,小球从开始到A:vA2-v02=-2as
由A到B,由机械能守恒定律有:
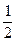 mvA2=
mvA2=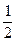 mvB2+2mgR
mvB2+2mgR
从B做平抛运动
sAC=vBt
2R=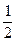 gt2
gt2
得sAC="1.2" m.
由A到B,由机械能守恒定律有:
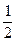 mvA2=
mvA2=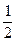 mvB2+2mgR
mvB2+2mgR从B做平抛运动
sAC=vBt
2R=
 gt2
gt2得sAC="1.2" m.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
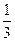 ,其余各处的摩擦不计,A、B、C均可视为质点,重力加速度为g.
,其余各处的摩擦不计,A、B、C均可视为质点,重力加速度为g.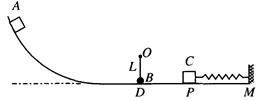
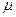 =0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求:
=0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求: