题目内容
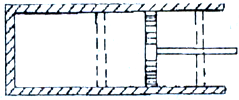
如图所示，一端开口的L形玻璃管是由粗细不同的两部分组成的，粗管的横截面积是细管横截面积的两倍（水平细管），开口管在竖直平面内，封闭端水平放置，水平段管长100cm，竖直段管长为30cm，在水平管内有一段长12cm的水银封闭着一段长80cm的空气柱，已知气柱的温度为27℃，大气压强为75cmHg，现对气体缓慢加热，当温度上升到119℃时，封闭端空气柱多长？分析：首先假设水银柱还全部在水平管内，此过程被封闭的气体压强不变，计算当温度变为119℃时，气体的长度，与水平管的长度相比较，判断是否合理．再假设进入竖直管的水银高度为xcm，分析此时的状态参量，列式进行求解．
解答：解：设细管的面积是S，则粗管的面积为2S，对被封闭的气体进行状态分析：
初状态：p1=75cmHg V1=80Scm3 T1=300K
当T2=392K时，假设水银仍在水平管内，则压强不变，由等压变化有：
=
V2=104.5Scm3＞100Scm3
不合理，故有水银已经到达竖直管．
设竖直管中水银的高度为xcm，进行状态分析，则有
p2=（75+x）cmHg V2=(88+2x)Scm3 T2=273+119=392K
由
=
代入数据有：
=
解得：x=5cm，
所以L2=88+2x=88+2×5=98cm
答：封闭端空气柱为98cm
初状态：p1=75cmHg V1=80Scm3 T1=300K
当T2=392K时，假设水银仍在水平管内，则压强不变，由等压变化有：
| V1 |
| T1 |
| V2 |
| T2 |
V2=104.5Scm3＞100Scm3
不合理，故有水银已经到达竖直管．
设竖直管中水银的高度为xcm，进行状态分析，则有
p2=（75+x）cmHg V2=(88+2x)Scm3 T2=273+119=392K
由
| p1V1 |
| T1 |
| p2V2 |
| T2 |
代入数据有：
| 75×80S |
| 300 |
| (75+x)(88+2x)S |
| 392 |
解得：x=5cm，
所以L2=88+2x=88+2×5=98cm
答：封闭端空气柱为98cm
点评：判断水银柱是否能进入竖直管是解决此问题的关键之一，要学会应用假设法来判断此问题；当有水银进入竖直管后，判断被封闭气体的压强也是解决此问题的关键，注意找出水平管内和竖直管内水银柱的长度的关系．是一道好题．
练习册系列答案
相关题目
如图所示，一端开口的圆筒中插入光滑活塞，密闭住一段理想气体，其状态参量为P0，V0，T0，在与外界无热交换的情况下，先压缩气体到p0，V1，T1状态，再让气体膨胀到p2，V2，T2状态，若V1＜V0＜V2，则（ ）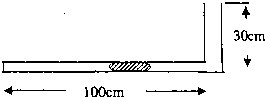
如图所示，一端开口的L形玻璃管是由粗细不同的两部分组成的，粗管的横截面积是细管横截面积的两倍，开口管在竖直平面内，封闭端水平放置，水平段管长100cm，竖直段管长为30cm，在水平管内有一段长12cm的水银封闭着一段长80cm的空气柱，已知气柱的温度为27℃，大气压强为75cm，现对气体缓慢加热，
