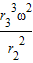题目内容
 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮的角速度为ω,则丙轮边缘上某点的向心加速度为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮的角速度为ω,则丙轮边缘上某点的向心加速度为( )分析:甲乙丙三个轮子的线速度相等,根据a=
求出丙轮边缘上某点的向心加速度.
| v2 |
| r |
解答:解:甲丙的线速度大小相等,根据a=
知甲丙的向心加速度之比为r3:r1,甲的向心加速度a甲=r1ω2,则a丙=
.故A正确,B、C、D错误.
故选A.
| v2 |
| r |
| r12ω2 |
| r3 |
故选A.
点评:解决本题的关键知道甲乙丙三个轮子具有相同的线速度大小,根据a=
可求出它们的向心加速度之比.
| v2 |
| r |

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
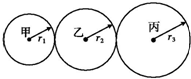 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,工作时哪个齿轮的角速度最大( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,工作时哪个齿轮的角速度最大( )| A、甲 | B、乙 | C、丙 | D、条件不足,无法判断 |


 B.
B.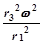 C.
C. D.
D.
 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮的角速度为ω,则丙轮边缘上某点的向心加速度为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮的角速度为ω,则丙轮边缘上某点的向心加速度为( )