题目内容
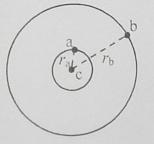
如图，三个质点a、b、c质量分别为m1、m2、M（M远大于m1，m2）．在C的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比ra：rb=1：4，从图示位置开始，在b运动一周的过程中，a、b、c共线了分析：质点a、b均在c点的万有引力的作用下绕c做圆周运动，由F引=F向，可求出周期比，每多转半圈，三质点共线一次，可先求出多转半圈的时间，与总时间相比，得出三点共线次数．
解答：解：万有引力提供向心力，则有：G
=m
r；
可得T=
因为轨道半径之比ra：rb=1：4
所以Ta：Tb=1：8；
设每隔时间t，a、b共线一次，则（ωa-ωb）t=π，所以t=
；
故b运动一周的过程中，a、b、c共线的次数为：n=
=
=
-2=14．
故答案为：14．
| Mm |
| r2 |
| 4π2 |
| T2 |
可得T=
|
因为轨道半径之比ra：rb=1：4
所以Ta：Tb=1：8；
设每隔时间t，a、b共线一次，则（ωa-ωb）t=π，所以t=
| π |
| ωa-ωb |
故b运动一周的过程中，a、b、c共线的次数为：n=
| Tb |
| t |
| Tb(ωa-ωb) |
| π |
| 2Tb |
| Ta |
故答案为：14．
点评：本题根据向心力来源列式，即可求出周期之比，可以以质点b、c系统为参考系，则a质点转动7圈，共线14次．
练习册系列答案
相关题目
（2010?上海）如图，三个质点a、b、c质量分别为m1、m2、M（M?m1，M?m2），在c的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比为ra：rb=1：4，则它们的周期之比Ta：Tb=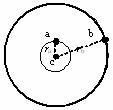
如图，三个质点a、b、c质量分别为m1、m2、M（M≫m1，M≫m2），在c的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比为ra:rb＝1:4，则它们的周期之比Ta:Tb＝__________，从图示位置开始，在b转动一周的过程中，a、b、c共线有__________次。
、
、
（
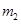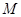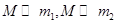）.在C的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比
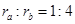,则它们的周期之比
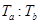=______;从图示位置开始，在b运动一周的过程中，a、b、c共线了____次。
、
、
（
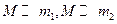）.在C的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比
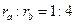,则它们的周期之比
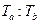=______;从图示位置开始，在b运动一周的过程中，a、b、c共线了____次。