题目内容
8.地球同步通信卫星绕地球做匀速圆周运动的周期与地球的自转周期相同,均为T.已知地球半径为R,地球表面的重力加速度为g.求:地球同步通信卫星的轨道半径.分析 根据角速度与周期的关系,地球同步卫星绕地球运行的角速度大小为ω=$\frac{2π}{T}$;再根据万有引力提供向心力G$\frac{mM}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r,地球表面的物体受到的重力等于万有引力G$\frac{M{m}_{0}}{{R}^{2}}$=m0g,解二方程即可得出r.
解答 解:设地球质量为M,卫星质量为m,引力常量为G,地球同步通信卫星的轨道半径为r,
则根据万有引力定律和牛顿第二定律有$G\frac{Mm}{r^2}=mr\frac{{4{π^2}}}{T^2}$
对于质量为m0的物体放在地球表面上,
根据万有引力定律有$G\frac{{M{m_0}}}{R^2}={m_0}g$
联立上述两式可解得$r=\root{3}{{\frac{{g{R^2}{T^2}}}{{4{π^2}}}}}$
答:地球同步通信卫星的轨道半径$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$.
点评 对万有引力与天体的运动问题,一定要知道两个关系:①星球表面的物体受到的重力等于万有引力,②做匀速圆周运动的物体需要的向心力由万有引力提供.熟练掌握这两个关系可以解决一切天体运动的问题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
18.洗衣机的脱水筒采用带动衣物旋转的方式脱水,下列说法中正确的是( )


| A. | 加快脱水筒转动角速度,脱水效果会更好 | |
| B. | 脱水过程中,衣物中昀水分是沿半径方向甩出去的 | |
| C. | 水会从衣物中甩出是因为水滴受到向心力很大的缘故 | |
| D. | 靠近中心的衣物脱水效果比靠近筒壁的衣物脱水效果好 |
19.在匀加速行驶的列车上,两个小球A,B均用细线拴接,细线另一端固定于车厢顶部,且相对于车厢保持静止.小球A的质量为mA,与竖直方向的夹角为αA,细线对小球A的拉力为FA;小球B的质量为mB,与竖直方向的夹角为αB,细线对小球B的拉力为FB.已知mA>mB,关于αA、αB及FA、FB的比较,下列结论正确的是( )
| A. | αA=αB,FA=FB | B. | αA=αB,FA>FB | C. | αA>αB,FA=FB | D. | αA>αB,FA>FB |
3.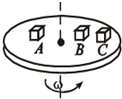 如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
 如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )| A. | 每个物体均受重力、支持力、静摩擦力、向心力四个力作用 | |
| B. | A的向心加速度大于B的向心加速度 | |
| C. | B和C所受摩擦力相等 | |
| D. | 若逐渐增大圆盘转速,C比B先滑动,A和B同时滑动 |
13.如图所示,直线a和曲线b分别是在同一条平直公路上行驶的汽车甲和汽车乙的v-t图线.由图可知( )


| A. | 在时刻t1,甲车和乙车处在同一位置 | |
| B. | 在时刻t2,甲、乙两车运动方向相反 | |
| C. | 在t1到t2这段时间内,乙车的加速度先减小后增大 | |
| D. | 在t1到t2这段时间内,甲车的位移小于乙车的位移 |
20.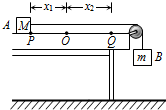 为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.
为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.
(1)请根据如表的实验数据在答题纸上的坐标图中作出x1-x2关系图象.
(2)木块与桌面之间的动摩擦因数μ=$\frac{{m{x_1}}}{{(M+m){x_2}+M{x_1}}}$(用M、m、x1、x2表示).
(3)实验中,细线与滑轮之间的摩擦以及滑轮轴的摩擦会导致的测量结果偏大(选填“偏大”、“偏小”或“无影响”).
 为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.
为测定木块与桌面之间的动摩擦因数,某同学设计了如图所示的装置进行实验.实验中,测得A、B的质量分别为M、m,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后由静止释放,B着地后速度立即减为零,A最终滑到Q点,分别测量OP、OQ的长度x1和x2.改变x1,重复上述实验,分别记录几组实验数据.(1)请根据如表的实验数据在答题纸上的坐标图中作出x1-x2关系图象.
| x1(cm) | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 |
| x2(cm) | 19.5 | 28.5 | 39.0 | 48.0 | 56.5 |
(3)实验中,细线与滑轮之间的摩擦以及滑轮轴的摩擦会导致的测量结果偏大(选填“偏大”、“偏小”或“无影响”).

 如图所示,在xOy平面内,第一象限中有匀强电场,场强大小为E,方向沿y轴正方向.在x轴的下方有匀强磁场,磁感应强度大小为B,方向垂直纸面向里.今有一个质量为m、电荷量为q的带负电的粒子(不计粒子的重力和其他阻力),从y轴上的P点以初速度v0垂直于电场方向进入电场.经电场偏转后,沿着与x轴正方向成30°角的方向进入磁场.
如图所示,在xOy平面内,第一象限中有匀强电场,场强大小为E,方向沿y轴正方向.在x轴的下方有匀强磁场,磁感应强度大小为B,方向垂直纸面向里.今有一个质量为m、电荷量为q的带负电的粒子(不计粒子的重力和其他阻力),从y轴上的P点以初速度v0垂直于电场方向进入电场.经电场偏转后,沿着与x轴正方向成30°角的方向进入磁场.