题目内容
5.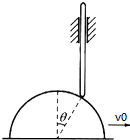 一个沿水平方向运动的半径为R的半圆柱体,在半圆柱面上搁着一根只能在竖直方向上运动的直杆(套在一个光滑的套管中),直杆的质量为m. 已知在半圆柱体速度为v0,加速度为a0时,杆与半圆柱体接触点的角位置为θ.如图所示,求此时半圆柱对竖直杆的支持力.
一个沿水平方向运动的半径为R的半圆柱体,在半圆柱面上搁着一根只能在竖直方向上运动的直杆(套在一个光滑的套管中),直杆的质量为m. 已知在半圆柱体速度为v0,加速度为a0时,杆与半圆柱体接触点的角位置为θ.如图所示,求此时半圆柱对竖直杆的支持力.
分析 根据运动的合成与分解规律可明确杆对地的速度和对地的加速度,再由牛顿第二定律可求得半圆柱对竖直杆的支持力.
解答 解:取半圆柱体为参照物,则v、a应为相对速度和相对加速度,竖直杆上的最低点P点相对于圆柱体的速度v相沿圆柱面上P点的切线方向,因此竖直杆的速度(相对于地面)应为v相和v的矢量和,如下图所示,由几何关系可知v相=vtanθ.圆柱体表面上P点的加速度由切向加速度at与法向加速度an组成,其中an=$\frac{{v}_{相}^{2}}{R}$,
即an=$\frac{{v}^{2}}{Rco{s}^{2}θ}$,P点的对地加速度为at、an的矢量和,
由图可知acosθ=a0sinθ-ancosθ
解得:a=a0tanθ--$\frac{{v}_{0}^{2}}{Rco{s}^{3}θ}$
对杆在竖直方向进行分析,由牛顿第二定律可知
F-mg=ma
解得:F=mg+ma0tanθ-m$\frac{{v}_{0}^{2}}{Rco{s}^{3}θ}$
答:此时半圆柱对竖直杆的支持力为mg+ma0tanθ-m$\frac{{v}_{0}^{2}}{Rco{s}^{3}θ}$
点评 本题考查运动的合成与分解,要注意明确P点相对于地面运动合速度可以看作是球运动的速度以及切向速度的合速度;同时注意速度、加速度及力等矢量均可以进行合成.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列说法正确的是( )
| A. | 速度变化越大,则加速度越大 | |
| B. | 加速度a<0,则物体一定减速运动 | |
| C. | 加速度a增大,则物体的速度一定增大 | |
| D. | 若加速度方向与速度方向相同,加速度减小时,则速度反而增大 |
1.如图所示,吊车以速度v1沿水平直线匀速行驶,同时以恒定速度v2收拢绳索提升物体,下列表述正确的是( )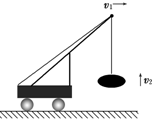

| A. | 绳索保持竖直状态 | B. | 物体的实际运动速度为(v1+v2) | ||
| C. | 物体相对地面做曲线运动 | D. | 绳索受到的拉力大于物体的重力 |
10.两束平行的光斜射到平行玻璃砖,经玻璃砖折射后如图所示,则关于这两束光的说法中正确的是( )

| A. | A光的折射率比B光的折射率小 | |
| B. | A光在水中的传播速度比B光在水中的传播速度小 | |
| C. | 从玻璃砖下表面射出的两束光可能不平行 | |
| D. | 若分别将这两束光用同一装置做双缝干涉实验,则A光在光屏上形成的条纹间距大 |
17.如图所示的光学现象中,下列的描述或解释错误的是( )


| A. | 图(a)中,小孔成的像是倒立的实像,反映了光在同种介质中沿直线传播 | |
| B. | 图(b)中,人配戴的凹透镜可以矫正近视眼,利用了光的折射原理 | |
| C. | 图(c)中,白光通过三棱镜可以分解成多种色光,是因为不同颜色的光通过玻璃时偏 折的角度不同 | |
| D. | 图(d)中,因漫反射的反射光线杂乱无章,因此有的光线可能不遵循光的反射定律 |
15.质点从静止开始沿直线运动,其位移-时间图象如图所示,则( )
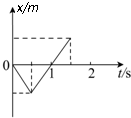

| A. | 在0到1 s时间内该质点的平均速率为零 | |
| B. | 在0到1 s时间内t=1 s时该质点回到出发点 | |
| C. | 在0到1 s时间内t=1 s时该质点瞬时速度为零 | |
| D. | 在0到1 s时间内t=0.5 s时该质点离出发点最远 |